
分析 (1)由题意可知椭圆的焦点在x轴上,c=$\sqrt{3}$,a2=3+b2,点$(-\sqrt{3},\frac{1}{2})$在椭圆C上,代入椭圆方程即可求得a和b的值,求得椭圆方程;
(2)过F2的直线斜率不为0,设l:x=my+$\sqrt{3}$,并代入椭圆方程,由韦达定理求得y1+y2和y1•y2,利用弦长公式求得丨AB丨,点到直线的距离公式求得F1到l的距离,利用三角形的面积公式及基本不等式的性质求得S△ABF1最大值,即可求得切圆M的面积最大值.
解答 解:(1)设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
由c=$\sqrt{3}$,a2=3+b2,又点$(-\sqrt{3},\frac{1}{2})$在椭圆C上,
$\frac{3}{3+{b}^{2}}+\frac{\frac{1}{4}}{{b}^{2}}=1$,即b2=1,a2=1,
∴$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(2)过F2的直线斜率不为0,设l:x=my+$\sqrt{3}$,与A(x1,y1)、B(x2,y2),将直线代入椭圆$\frac{{x}^{2}}{4}+{y}^{2}=1$得:
(m2+4)y2+2$\sqrt{3}$my-1=0,
∴y1+y2=$\frac{-2\sqrt{3}m}{{m}^{2}+4}$,y1•y2=$\frac{-1}{{m}^{2}+4}$,
丨AB丨=$\sqrt{(1+{m}^{2})[(\frac{2\sqrt{3}m}{{m}^{2}+4})^{2}+\frac{4}{{m}^{2}+4}]}$=$\sqrt{(1+{m}^{2})×\frac{16{m}^{2}+16}{({m}^{2}+4)^{2}}}$=$\frac{4({m}^{2}+1)}{{m}^{2}+4}$,
点F1(-$\sqrt{3}$,0)到l:x=my+$\sqrt{3}$,的距离为d=$\frac{2\sqrt{3}}{\sqrt{1+{m}^{2}}}$,
S△ABF1=$\frac{1}{2}$×$\frac{2\sqrt{3}}{\sqrt{1+{m}^{2}}}$×$\frac{4({m}^{2}+1)}{{m}^{2}+4}$=$\frac{4\sqrt{3}\sqrt{1+{m}^{2}}}{{m}^{2}+4}$=4$\sqrt{3}$$\sqrt{\frac{1+{m}^{2}}{({m}^{2}+4)^{2}}}$,
=4$\sqrt{3}$$\sqrt{\frac{1}{({m}^{2}+1)+\frac{9}{{m}^{2}+1}+6}}$≤4$\sqrt{3}$×$\sqrt{\frac{1}{12}}$=2,
当且仅当m2+1=$\frac{9}{{m}^{2}+1}$,即m=±$\sqrt{2}$时取等,
设内切圆M的半径为r,则S△ABF1=$\frac{1}{2}$×rmax×4a=4r=2,即rmax=$\frac{1}{2}$,
即内切圆M的面积最大值为:S圆Mmax=πr2=$\frac{π}{4}$.
点评 本题考查椭圆的标准方程及性质,考查了直线和圆锥曲线的位置关系,考查韦达定理的运用、弦长公式、点到直线的距离公式,考查计算能力,是中档题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:解答题
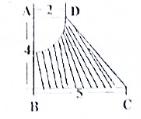
如图,四边形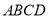 为梯形,
为梯形,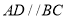 ,
,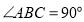 ,求图中阴影部分绕
,求图中阴影部分绕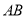 旋转一周形成的几何体的表面积和体积.
旋转一周形成的几何体的表面积和体积.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:选择题
已知圆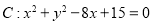 ,直线
,直线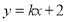 上至少存在一点
上至少存在一点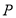 ,使得以点
,使得以点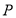 为原心,半径为1的圆与圆
为原心,半径为1的圆与圆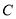 有公共点,则
有公共点,则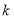 的最小值是( )
的最小值是( )
A.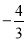 B.
B.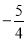 C.
C.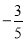 D.
D.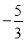
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
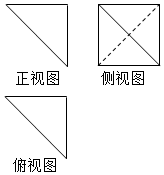 某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的外接球的体积是( )
某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的外接球的体积是( )| A. | 12π | B. | 48π | C. | 4$\sqrt{3}$π | D. | 32$\sqrt{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
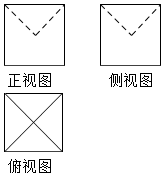 某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,两条虚线互相垂直且相等,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,两条虚线互相垂直且相等,则该几何体的体积是( )| A. | $\frac{20}{3}$ | B. | $\frac{16}{3}$ | C. | $8-\frac{π}{6}$ | D. | $8-\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
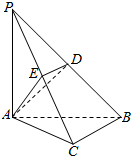 如图,在三棱锥P-ABC中,PA⊥底面ABC,点D,E分别在棱PB、PC上,PA=AB=2,∠ABC=60°,∠BCA=90°,且DE∥BC.
如图,在三棱锥P-ABC中,PA⊥底面ABC,点D,E分别在棱PB、PC上,PA=AB=2,∠ABC=60°,∠BCA=90°,且DE∥BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com