

 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原 ;
; 个元件,寿命为
个元件,寿命为 之间的应抽取几个;
之间的应抽取几个; 之间的元件中任取
之间的元件中任取 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为 ,一个寿命为
,一个寿命为 ”的概率.
”的概率.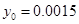 ;(2)应抽取
;(2)应抽取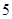 个;(3)
个;(3)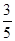 .
. ;第二问,利用“频率=频数÷样本总数”计算寿命为
;第二问,利用“频率=频数÷样本总数”计算寿命为 之间应抽取的个数;第三问,分别设出寿命为
之间应抽取的个数;第三问,分别设出寿命为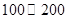 之间的2个元件和
之间的2个元件和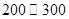 之间的3个元件,先写出从5个元件中任取2个元件的所有情况,再从中选出符合题意的种数,两个种数相除得到概率的值.
之间的3个元件,先写出从5个元件中任取2个元件的所有情况,再从中选出符合题意的种数,两个种数相除得到概率的值.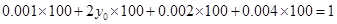
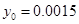 3分
3分 之间的应抽取
之间的应抽取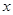 个,根据分层抽样有:
个,根据分层抽样有: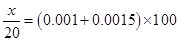 5分
5分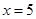
 之间的应抽取
之间的应抽取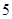 个 7分
个 7分 ,一个寿命为
,一个寿命为 ”为事件
”为事件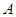 ,由(2)知
,由(2)知  之间的元件有
之间的元件有 个分别记
个分别记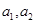 ,落在
,落在 之间的元件有
之间的元件有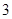 个分别记为:
个分别记为: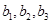 ,从中任取
,从中任取 个球,有如下基本事件:
个球,有如下基本事件: 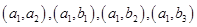 ,
,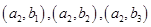 ,
, 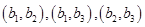 ,共有
,共有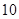 个基本事件 9分
个基本事件 9分 “恰好有一个寿命为
“恰好有一个寿命为 ,一个寿命为
,一个寿命为 ”有:
”有: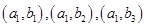 ,
,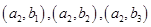 共有
共有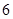 个基本事件 10分
个基本事件 10分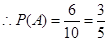 11分
11分 ,另一个寿命为
,另一个寿命为 ”的概率为
”的概率为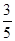 . 12分
. 12分

科目:高中数学 来源:不详 题型:解答题
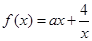 .
.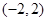 内任取一个实数
内任取一个实数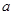 ,设事件
,设事件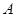 ={函数
={函数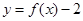 在区间
在区间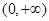 上有两个不同的零点},求事件
上有两个不同的零点},求事件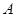 发生的概率;
发生的概率;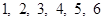 )得到的点数分别为
)得到的点数分别为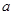 和
和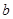 ,记事件
,记事件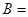 {
{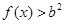 在
在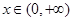 恒成立},求事件
恒成立},求事件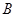 发生的概率.
发生的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 表示开始第4次发球时乙的得分,求
表示开始第4次发球时乙的得分,求 的期望.
的期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.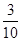 | B.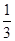 | C.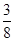 | D.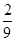 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
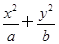 =1表示焦点在x轴上的椭圆的概率为________.
=1表示焦点在x轴上的椭圆的概率为________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com