
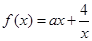 .
.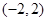 内任取一个实数
内任取一个实数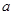 ,设事件
,设事件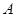 ={函数
={函数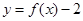 在区间
在区间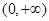 上有两个不同的零点},求事件
上有两个不同的零点},求事件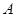 发生的概率;
发生的概率;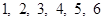 )得到的点数分别为
)得到的点数分别为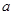 和
和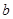 ,记事件
,记事件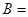 {
{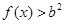 在
在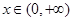 恒成立},求事件
恒成立},求事件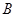 发生的概率.
发生的概率. 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源:不详 题型:解答题

 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原 ;
; 个元件,寿命为
个元件,寿命为 之间的应抽取几个;
之间的应抽取几个; 之间的元件中任取
之间的元件中任取 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为 ,一个寿命为
,一个寿命为 ”的概率.
”的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 )分成六段
)分成六段 ,
, ,
, ,
, ,
, ,
, 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图. 的车辆为
的车辆为 ,
, , ,
, , (
( 为车速在
为车速在 上的频数),车速在
上的频数),车速在 的车辆为
的车辆为 ,
, , ,
, , (
( 为车速在
为车速在 上的频数),从车速在
上的频数),从车速在 的车辆中任意抽取
的车辆中任意抽取 辆共有几种情况?请列举出所有的情况,并求抽取的
辆共有几种情况?请列举出所有的情况,并求抽取的 辆车的车速都在
辆车的车速都在 上的概率.
上的概率.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
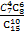 的是( )
的是( )| A.P(X=2) | B.P(X≤2) |
| C.P(X=4) | D.P(X≤4) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0.42 | B.0.28 | C.0.3 | D.0.7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com