
 )分成六段
)分成六段 ,
, ,
, ,
, ,
, ,
, 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图. 的车辆为
的车辆为 ,
, , ,
, , (
( 为车速在
为车速在 上的频数),车速在
上的频数),车速在 的车辆为
的车辆为 ,
, , ,
, , (
( 为车速在
为车速在 上的频数),从车速在
上的频数),从车速在 的车辆中任意抽取
的车辆中任意抽取 辆共有几种情况?请列举出所有的情况,并求抽取的
辆共有几种情况?请列举出所有的情况,并求抽取的 辆车的车速都在
辆车的车速都在 上的概率.
上的概率.
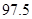 ;(2)
;(2)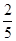
 的车辆频率为0.05,车速在
的车辆频率为0.05,车速在 的车辆的频率为0.1.所以可求出车速在这两段上的车辆数.再求出相应的概率即可.
的车辆的频率为0.1.所以可求出车速在这两段上的车辆数.再求出相应的概率即可. ,
, ,
, ,
, 上的频率分别为
上的频率分别为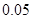 ,
,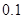 ,
,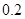 ,
,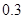 ;
;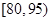 上的频率是
上的频率是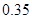 ,车速在区间
,车速在区间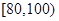 上的频率是
上的频率是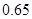 .
. 内. 2分
内. 2分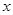 ,
, .
.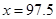 .
.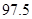 6分
6分 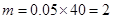 ,
,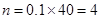 . 8分
. 8分 的车辆中任意抽取
的车辆中任意抽取 辆的所有情况是:
辆的所有情况是: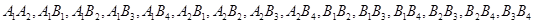 ,共有
,共有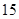 种情况. 10分
种情况. 10分 上的
上的 辆车的情况有
辆车的情况有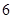 种.所以车速都在
种.所以车速都在 上的
上的 辆车的概率是
辆车的概率是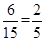 . 12分
. 12分

 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源:不详 题型:解答题
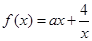 .
.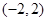 内任取一个实数
内任取一个实数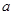 ,设事件
,设事件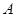 ={函数
={函数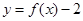 在区间
在区间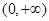 上有两个不同的零点},求事件
上有两个不同的零点},求事件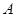 发生的概率;
发生的概率;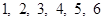 )得到的点数分别为
)得到的点数分别为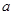 和
和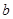 ,记事件
,记事件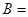 {
{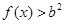 在
在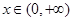 恒成立},求事件
恒成立},求事件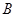 发生的概率.
发生的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 表示开始第4次发球时乙的得分,求
表示开始第4次发球时乙的得分,求 的期望.
的期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
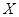 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量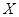 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 车尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
| 限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为 ,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立,假设该射手完成以上三次射击.
,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立,假设该射手完成以上三次射击.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com