
| 车尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
| 限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
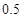 ;(2)所以
;(2)所以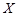 的的分布列为
的的分布列为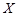 | 0 | 1 | 2 | 3 |
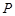 | 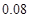 | 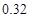 | 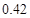 | 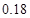 |
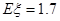 .
.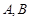 两车是否出车相互独立,有互斥事件与独立事件的概率求法,即可求出该单位在星期一恰好出一台车的概率;(2)由于星期二限行尾号为6的车,故
两车是否出车相互独立,有互斥事件与独立事件的概率求法,即可求出该单位在星期一恰好出一台车的概率;(2)由于星期二限行尾号为6的车,故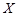 的可能取值为0,1,2,3,分别求出概率,可得分布列,进而可求出期望.
的可能取值为0,1,2,3,分别求出概率,可得分布列,进而可求出期望.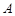 车在星期
车在星期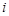 出车的事件为
出车的事件为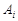 ,
,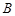 车在星期
车在星期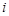 出车的事件为
出车的事件为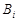 ,
,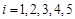
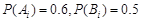
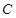 , 1分
, 1分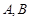 两车是否出车相互独立,且事件
两车是否出车相互独立,且事件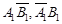 互斥 2分
互斥 2分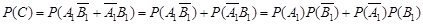
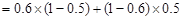 4分
4分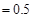
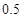 . 5分
. 5分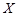 的可能取值为0,1,2,3 6分
的可能取值为0,1,2,3 6分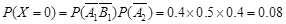
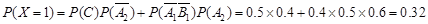
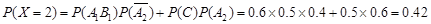
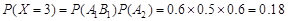 10分
10分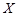 的的分布列为
的的分布列为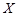 | 0 | 1 | 2 | 3 |
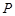 | 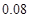 | 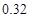 | 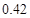 | 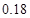 |
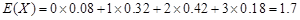 13分
13分

科目:高中数学 来源:不详 题型:解答题

 表示在这块地上种植1季此作物的利润,求
表示在这块地上种植1季此作物的利润,求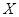 的分布列;
的分布列;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
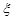 ,求随机变量
,求随机变量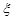 的分布列及其期望.
的分布列及其期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (如图)这六个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为
(如图)这六个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为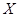 ,若
,若 就去打球,若
就去打球,若 就去唱歌,若
就去唱歌,若 就去下棋。
就去下棋。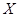 的所有可能值;
的所有可能值;
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
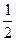 ,从开关第二次闭合起,若前次出现红灯,则下一次出现红灯的概率是
,从开关第二次闭合起,若前次出现红灯,则下一次出现红灯的概率是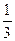 ,出现绿灯的概率是
,出现绿灯的概率是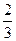 ;若前次出现绿灯,则下一次出现红灯的概率是
;若前次出现绿灯,则下一次出现红灯的概率是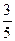 ,出现绿灯的概率是
,出现绿灯的概率是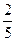 ,则三次发光中,出现一次红灯、两次绿灯的概率是( )
,则三次发光中,出现一次红灯、两次绿灯的概率是( )A.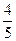 | B.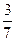 | C.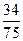 | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 )分成六段
)分成六段 ,
, ,
, ,
, ,
, ,
, 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图. 的车辆为
的车辆为 ,
, , ,
, , (
( 为车速在
为车速在 上的频数),车速在
上的频数),车速在 的车辆为
的车辆为 ,
, , ,
, , (
( 为车速在
为车速在 上的频数),从车速在
上的频数),从车速在 的车辆中任意抽取
的车辆中任意抽取 辆共有几种情况?请列举出所有的情况,并求抽取的
辆共有几种情况?请列举出所有的情况,并求抽取的 辆车的车速都在
辆车的车速都在 上的概率.
上的概率.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 射击环数 | 频数 | 频率 |
| 7 | 10 | 0.1 |
| 8 | 10 | 0.1 |
| 9 | x | 0.45 |
| 10 | 35 | y |
| 合计 | 100 | 1 |
| 射击环数 | 频数 | 频率 |
| 7 | 8 | 0.1 |
| 8 | 12 | 0.15 |
| 9 | z | |
| 10 | | 0.35 |
| 合计 | 80 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com