
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴非负半轴上,点
轴非负半轴上,点![]() 满足:
满足:![]()
(1)当点![]() 在
在![]() 轴上移动时,求动点
轴上移动时,求动点![]() 的轨迹C的方程;
的轨迹C的方程;
(2)设![]() 为曲线C上一点,直线
为曲线C上一点,直线![]() 过点
过点![]() 且与曲线C在点
且与曲线C在点![]() 处的切线垂直,
处的切线垂直,![]() 与C的另一个交点为
与C的另一个交点为![]() ,若以线段
,若以线段![]() 为直径的圆经过原点,求直线
为直径的圆经过原点,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
试题分析:(1)由点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴非负半轴上且为动点,可设出设A(a,0),B(0,b),M(x,y),由关系
轴非负半轴上且为动点,可设出设A(a,0),B(0,b),M(x,y),由关系![]() ,将向量坐标代入可得动点
,将向量坐标代入可得动点![]() 的轨迹C的方程.
的轨迹C的方程.
(2)设Q(m,2m2), 直线![]() 过点
过点![]() 且与曲线C在点
且与曲线C在点![]() 处的切线垂直,可求出直线l的方程为y﹣2m2=
处的切线垂直,可求出直线l的方程为y﹣2m2=![]() (x﹣m),设
(x﹣m),设![]() ,联立
,联立![]() 与C的方程,并由韦达定理可得
与C的方程,并由韦达定理可得![]() ,
,![]() , (2m2)yR,2m2
, (2m2)yR,2m2![]() yR,又由线段
yR,又由线段![]() 为直径的圆经过原点,所以
为直径的圆经过原点,所以![]() ,即mxR+(2m2)yR=0,整理后可求出直线
,即mxR+(2m2)yR=0,整理后可求出直线![]() 的方程.
的方程.
试题解析:
解:(Ⅰ)设A(a,0),M(x,y),B(0,b),则![]() =(x﹣a,y),
=(x﹣a,y),![]() =(﹣a,b),
=(﹣a,b),![]() =(a,1)
=(a,1)
∵![]() =2
=2![]() ,∴有(x﹣a,y)=2(﹣a,b),即有x﹣a=﹣2a,y=2b,即x=﹣a,y=2b
,∴有(x﹣a,y)=2(﹣a,b),即有x﹣a=﹣2a,y=2b,即x=﹣a,y=2b
∵![]() ,∴有a(x﹣a)+y=0
,∴有a(x﹣a)+y=0
∴﹣x(x+x)+y=0,∴﹣2x2+y=0
即C的方程是y=2x2;
(Ⅱ)设Q(m,2m2),直线l的斜率为k,则y′=4x,∴k=![]()
∴直线l的方程为y﹣2m2=![]() (x﹣m)
(x﹣m)
与y=2x2联立,消去y可得2x2+![]() x﹣2m2﹣
x﹣2m2﹣![]() =0,该方程必有两根m与xR,且mxR=﹣m2﹣
=0,该方程必有两根m与xR,且mxR=﹣m2﹣![]()
∴(2m2)yR=4(﹣m2﹣![]() )2
)2
∵![]() ,∴mxR+(2m2)yR=0,∴﹣m2﹣
,∴mxR+(2m2)yR=0,∴﹣m2﹣![]() +4(﹣m2﹣
+4(﹣m2﹣![]() )2=0,∴m=±
)2=0,∴m=±![]()
∴直线l的方程为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在正四面体A—BCD中,棱长为4,M是BC的中点,
点P在线段AM上运动(P不与A、M重合),过
点P作直线l⊥平面ABC,l与平面BCD交于点Q,
给出下列命题:
①BC⊥平面AMD ②Q点一定在直线DM上
③![]()
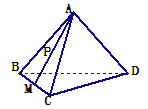
其中正确的是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公差为正数的等差数列,其前
是公差为正数的等差数列,其前![]() 项和为
项和为![]() ,
,
且![]() ,
,![]()
(1)求数列![]() 的通项公式.
的通项公式.
(2)设数列![]() 满足
满足![]() ,
,![]()
①求数列![]() 的通项公式;
的通项公式;
②是否存在正整数![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,侧面
,侧面![]() 为正三角形,侧面
为正三角形,侧面![]() 底面
底面![]() ,
,![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 的中点.
的中点.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的离心率为
的离心率为![]() ,点
,点![]() 为左焦点,过点
为左焦点,过点![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于
于![]() 、
、![]() 两点,且
两点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)在圆![]() 上是否存在一点
上是否存在一点![]() ,使得在点
,使得在点![]() 处的切线
处的切线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点满足
两点满足![]() ?若存在,求
?若存在,求![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com