
【题目】已知椭圆![]() :
:![]()
![]() 的离心率为
的离心率为![]() ,点
,点![]() 为左焦点,过点
为左焦点,过点![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于
于![]() 、
、![]() 两点,且
两点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)在圆![]() 上是否存在一点
上是否存在一点![]() ,使得在点
,使得在点![]() 处的切线
处的切线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点满足
两点满足![]() ?若存在,求
?若存在,求![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)![]() (2) 在圆上不存在这样的点
(2) 在圆上不存在这样的点![]() 使其成立
使其成立
【解析】
试题分析:(1)根据椭圆的离心率公式和通径的表达式![]() ,构造方程,得到椭圆方程;(2)将向量的位置关系,坐标化为
,构造方程,得到椭圆方程;(2)将向量的位置关系,坐标化为![]() ,得到两个变量的等量关系,联立直线和椭圆,将向量的位置关系,根据韦达定理,坐标化为
,得到两个变量的等量关系,联立直线和椭圆,将向量的位置关系,根据韦达定理,坐标化为![]() ,再根据直线和圆的位置关系得到
,再根据直线和圆的位置关系得到![]() ,联立这两个方程,二元化一元,得到方程无解,故不存在。
,联立这两个方程,二元化一元,得到方程无解,故不存在。
解析:
(1)![]()
又![]()
![]() ,
,![]()
![]() 椭圆
椭圆![]() 的方程为:
的方程为:![]()
(2)假设存在点![]() ,使得
,使得![]() .当
.当![]() 的斜率不存在时,
的斜率不存在时,![]() :
:![]() 或
或![]()
与椭圆![]() :
:![]() 相交于
相交于![]() ,
,![]() 两点,
两点,
此时![]()
![]() 或
或![]()
![]()
![]()
![]()
![]() 当直线
当直线![]() 的斜率不存在时不满足.
的斜率不存在时不满足.
当直线![]() 的斜率存在时,设:
的斜率存在时,设:![]()
则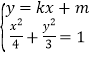
![]()
![]()
![]() 直线
直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点
两点
![]() ,化简得
,化简得![]()
设![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
又![]() 与圆
与圆![]() 相切,
相切,![]()
![]()
![]()
![]() ,显然不成立,
,显然不成立,![]() 在圆上不存在这样的点
在圆上不存在这样的点![]() 使其成立.
使其成立.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】某市公园内的人工湖上有一个以点![]() 为圆心的圆形喷泉,沿湖有一条小径
为圆心的圆形喷泉,沿湖有一条小径![]() ,在
,在![]() 的另一侧建有控制台
的另一侧建有控制台![]() ,
,![]() 和
和![]() 之间均有小径连接(小径均为直路),且
之间均有小径连接(小径均为直路),且![]() ,喷泉中心
,喷泉中心![]() 点距离
点距离![]() 点60米,且
点60米,且![]() 连线恰与
连线恰与![]() 平行,在小径
平行,在小径![]() 上有一拍照点
上有一拍照点![]() ,现测得
,现测得![]() 米,
米, ![]() 米,且
米,且![]() .
.
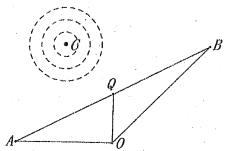
(I)请计算小径![]() 的长度;
的长度;
(Ⅱ)现打算改建控制台![]() 的位置,其离喷泉尽可能近,在点
的位置,其离喷泉尽可能近,在点![]() 的位置及
的位置及![]() 大小均不变的前提下,请计算
大小均不变的前提下,请计算![]() 距离的最小值;
距离的最小值;
(Ⅲ)一人从小径一端![]() 处向
处向![]() 处匀速前进时,喷泉恰好同时开启,喷泉开启
处匀速前进时,喷泉恰好同时开启,喷泉开启![]() 分钟后的水幕是一个以
分钟后的水幕是一个以![]() 为圆心,半径
为圆心,半径![]() 米的圆形区域(含边界),此人的行进速度是
米的圆形区域(含边界),此人的行进速度是![]() 米/分钟,在这个人行进的过程中他会被水幕沾染,试求实数
米/分钟,在这个人行进的过程中他会被水幕沾染,试求实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴非负半轴上,点
轴非负半轴上,点![]() 满足:
满足:![]()
(1)当点![]() 在
在![]() 轴上移动时,求动点
轴上移动时,求动点![]() 的轨迹C的方程;
的轨迹C的方程;
(2)设![]() 为曲线C上一点,直线
为曲线C上一点,直线![]() 过点
过点![]() 且与曲线C在点
且与曲线C在点![]() 处的切线垂直,
处的切线垂直,![]() 与C的另一个交点为
与C的另一个交点为![]() ,若以线段
,若以线段![]() 为直径的圆经过原点,求直线
为直径的圆经过原点,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知直线l:x﹣y+4=0和圆O:x2+y2=4,P是直线l上一点,过点P作圆C的两条切线,切点分别为M,N.
(1)若PM⊥PN,求点P坐标;
(2)若圆O上存在点A,B,使得∠APB=60°,求点P的横坐标的取值范围;
(3)设线段MN的中点为Q,l与x轴的交点为T,求线段TQ长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,且
上,且![]() ,其中
,其中![]() ,连接
,连接![]() ,延长
,延长![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 时,求二面角
时,求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求
时,求![]() 值.
值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com