
【题目】在正四面体A—BCD中,棱长为4,M是BC的中点,
点P在线段AM上运动(P不与A、M重合),过
点P作直线l⊥平面ABC,l与平面BCD交于点Q,
给出下列命题:
①BC⊥平面AMD ②Q点一定在直线DM上
③![]()
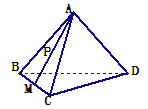
其中正确的是( )
A.①②B.①③C.②③D.①②③
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在R上的偶函数,且f(x+2)=f(2-x),当x∈[-2,0]时,f(x)= ,则在区间(-2,6)上关于x的方程f(x)-log8(x+2)=0的解的个数为( )
,则在区间(-2,6)上关于x的方程f(x)-log8(x+2)=0的解的个数为( )
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市公园内的人工湖上有一个以点![]() 为圆心的圆形喷泉,沿湖有一条小径
为圆心的圆形喷泉,沿湖有一条小径![]() ,在
,在![]() 的另一侧建有控制台
的另一侧建有控制台![]() ,
,![]() 和
和![]() 之间均有小径连接(小径均为直路),且
之间均有小径连接(小径均为直路),且![]() ,喷泉中心
,喷泉中心![]() 点距离
点距离![]() 点60米,且
点60米,且![]() 连线恰与
连线恰与![]() 平行,在小径
平行,在小径![]() 上有一拍照点
上有一拍照点![]() ,现测得
,现测得![]() 米,
米, ![]() 米,且
米,且![]() .
.
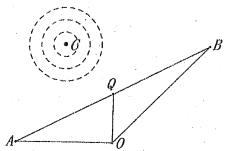
(I)请计算小径![]() 的长度;
的长度;
(Ⅱ)现打算改建控制台![]() 的位置,其离喷泉尽可能近,在点
的位置,其离喷泉尽可能近,在点![]() 的位置及
的位置及![]() 大小均不变的前提下,请计算
大小均不变的前提下,请计算![]() 距离的最小值;
距离的最小值;
(Ⅲ)一人从小径一端![]() 处向
处向![]() 处匀速前进时,喷泉恰好同时开启,喷泉开启
处匀速前进时,喷泉恰好同时开启,喷泉开启![]() 分钟后的水幕是一个以
分钟后的水幕是一个以![]() 为圆心,半径
为圆心,半径![]() 米的圆形区域(含边界),此人的行进速度是
米的圆形区域(含边界),此人的行进速度是![]() 米/分钟,在这个人行进的过程中他会被水幕沾染,试求实数
米/分钟,在这个人行进的过程中他会被水幕沾染,试求实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C过点M(0,-2)、N(3,1),且圆心C在直线x+2y+1=0上.
(1)求圆C的方程;
(2)设直线ax-y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面使用类比推理正确的是( )
A. 直线a∥b,b∥c,则a∥c,类推出:向量![]() ,则
,则![]()
B. 同一平面内,直线a,b,c,若a⊥c,b⊥c,则a∥b.类推出:空间中,直线a,b,c,若a⊥c,b⊥c,则a∥b
C. 实数a,b,若方程x2+ax+b=0有实数根,则a2≥4b.类推出:复数a,b,若方程x2+ax+b=0有实数根,则a2≥4b
D. 以点(0,0)为圆心,r为半径的圆的方程为x2+y2=r2.类推出:以点(0,0,0)为球心,r为半径的球的方程为x2+y2+z2=r2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴非负半轴上,点
轴非负半轴上,点![]() 满足:
满足:![]()
(1)当点![]() 在
在![]() 轴上移动时,求动点
轴上移动时,求动点![]() 的轨迹C的方程;
的轨迹C的方程;
(2)设![]() 为曲线C上一点,直线
为曲线C上一点,直线![]() 过点
过点![]() 且与曲线C在点
且与曲线C在点![]() 处的切线垂直,
处的切线垂直,![]() 与C的另一个交点为
与C的另一个交点为![]() ,若以线段
,若以线段![]() 为直径的圆经过原点,求直线
为直径的圆经过原点,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知直线l:x﹣y+4=0和圆O:x2+y2=4,P是直线l上一点,过点P作圆C的两条切线,切点分别为M,N.
(1)若PM⊥PN,求点P坐标;
(2)若圆O上存在点A,B,使得∠APB=60°,求点P的横坐标的取值范围;
(3)设线段MN的中点为Q,l与x轴的交点为T,求线段TQ长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com