
【题目】在斜三棱柱ABC﹣A1B1C1中,底面ABC是正三角形,E是AB中点,A1E⊥平面ABC.
(I)证明:BC1∥平面 A1EC;
(II)若A1A⊥A1B,且AB=2.
①求点B到平面ACC1A1的距离;
②求直线CB1与平面ACC1A1所成角的正弦值.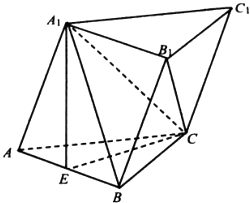
【答案】解:(I)证明:设AC1与A1C交于F点,连接EF,
∵E,F分别是线段AB,AC1的中点,
∴EF∥BC1 , 又EF平面 A1EC,BC1平面A1EC
故 BC1∥平面A1EC,
(II)①在正三角形A BC中,过E作E H⊥AC于H,连接A1H
显然AC⊥平面A1EH,
∵AC平面ACC1A1
∴平面A1EH⊥平面ACC1A1 , 且两个平面的交线为A1H
过E作EG⊥A1H于G,则EG⊥平面ACC1A1
在Rt△AA1B中,由已知易得A1E=1,在正三角形ABC中, ![]()
则在Rt△A1E H中, 
即点E到平面ACC1A1的距离为 ![]() ,
,
∵E是线段AB中点,
∴点B到平面ACC1A1的距离 ![]() ,
,
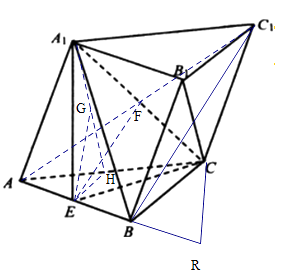
②延长EB至R点,使EB=BR=1,连接RC,
∴B1R∥A1E,则B1R⊥平面ARC,即有B1R⊥RC
在△BRC中易得 ![]() ,
,
∴ ![]()
设直线B1C与平面ACC1A1所成角为φ
则 ![]() .
.
【解析】(Ⅰ)根据线面平行的判定定理进行证明即可.(Ⅱ)根据点到平面的距离公式以及线面角的定义,结合三角形的边角关系进行求解.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则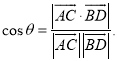 .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a(x﹣1)2+lnx+1,g(x)=f(x)﹣x,其中a∈R.
(Ⅰ)当a=﹣ ![]() 时,求函数f(x)的极值;
时,求函数f(x)的极值;
(Ⅱ)当a>0时,求函数g(x)的单调区间;
(Ⅲ)当x∈[1,+∞)时,若y=f(x)图象上的点都在 ![]() 所表示的平面区域内,求实数a的取值范围.
所表示的平面区域内,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在斜三棱柱ABC﹣A1B1C1中,底面ABC是正三角形,E是AB中点,A1E⊥平面ABC.
(I)证明:BC1∥平面 A1EC;
(II)若A1A⊥A1B,且AB=2.
①求点B到平面ACC1A1的距离;
②求直线CB1与平面ACC1A1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,在点M(1,f(1))处的切线方程为9x+3y-10=0,求
,在点M(1,f(1))处的切线方程为9x+3y-10=0,求
(1)实数a,b的值;
(2)函数f(x)的单调区间以及在区间[0,3]上的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex , g(x)=kx+1.
(I)求函数y=f(x)﹣(x+1)的最小值;
(II)证明:当k>1时,存在x0>0,使对于任意x∈(0,x0)都有f(x)<g(x);
(III)若存在实数m使对任意x∈(0,m)都有|f(x)﹣g(x)|>x成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={(x,y)|y=f(x)},若对于任意(x1 , y1)∈M,存在(x2 , y2)∈M,使得x1x2+y1y2=0成立,则称集合M是“垂直对点集”.给出下列四个集合:
①M={ ![]() };
};
②M={(x,y)|y=sinx+1};
③M={(x,y)|y=log2x};
④M={(x,y)|y=ex﹣2}.
其中是“垂直对点集”的序号是( )
A.①②
B.②③
C.①④
D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com