
分析 由题意求得数列{an}的通项公式,将原不等式转化成n2-tn-2t2≤0,构造辅助函数f(x)=n2-tn-2t2,由题意可知f(1)≤0,f(2)>0,即可求得t的取值范围.
解答 解:当n≥2时,an=Sn-Sn-1=$\frac{(n+1){a}_{n}}{2}$-$\frac{n{a}_{n-1}}{2}$,
整理得$\frac{{a}_{n}}{n}$=$\frac{{a}_{n-1}}{n-1}$,又a1=1,故an=n,
不等式an2-tan-2t2≤0可化为:n2-tn-2t2≤0,
设f(n)=n2-tn-2t2,由于f(0)=-2t2,
由题意可得:$\left\{\begin{array}{l}{f(1)=1-t-2{t}^{2}≤0}\\{f(2)=4-2t-2{t}^{2}>0}\end{array}\right.$,解得-2<t≤-1或$\frac{1}{2}$≤t<1.
故答案为:-2<t≤-1或$\frac{1}{2}$≤t<1.
点评 本题考查了数列的递推关系、不等式的性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
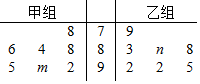 某市重点中学奥数培训班共有14人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则m+n的值是( )
某市重点中学奥数培训班共有14人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则m+n的值是( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
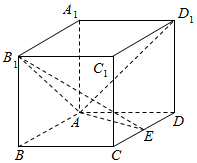 如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,E为CD上任意一点.
如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,E为CD上任意一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$π | B. | 4π | C. | 2π+2$\sqrt{5}$π | D. | 5π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2014 | B. | 2016 | C. | 3042 | D. | 4027 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com