
如图,直三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC。若AB=AC=AA1=1,BC=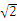 ,则异面直线A1C与B1C1所成的角为
,则异面直线A1C与B1C1所成的角为
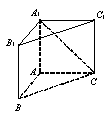
A.30° B.45° C.60° D.90°
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
已知抛物线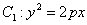 上一点
上一点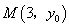 到其焦点
到其焦点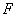 的距离为4;椭圆
的距离为4;椭圆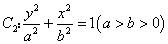 的离心率
的离心率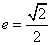 ,且过抛物线的焦点
,且过抛物线的焦点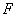 .
.
(I)求抛物线 和椭圆
和椭圆 的标准方程;
的标准方程;
(II)过点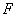 的直线
的直线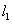 交抛物线
交抛物线 于
于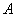 、
、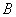 两不同点,交
两不同点,交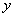 轴于点
轴于点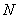 ,已知
,已知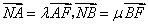 ,求证:
,求证: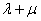 为定值.
为定值.
(III)直线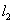 交椭圆
交椭圆 于
于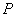 ,
,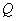 两不同点,
两不同点,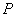 ,
,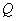 在
在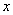 轴的射影分别为
轴的射影分别为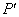 ,
,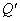 ,
,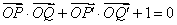 ,若点S满足:
,若点S满足: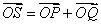 ,证明:点S在椭圆
,证明:点S在椭圆 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
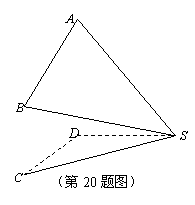
如图,在几何体SABCD中,AD⊥平面SCD,BC⊥
平面SCD,AD=DC=2,BC=1,又SD=2,∠SDC=120°.
(1)求SC与平面SAB所成角的正弦值;
(2)求平面SAD与平面SAB所成的锐二面角的余弦值.
 |
查看答案和解析>>
科目:高中数学 来源: 题型:
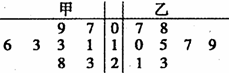
某篮球队甲、乙两名队员在本赛季已结束的80 场比赛中得分统计的茎叶图如图.
(1)比较这两名队员在比赛中得分的均值和方
差的大小;
(2)从乙比赛得分在20分以下的6场比赛中随机抽取2场进行失误分析,求抽到恰好
有1场得分不足10分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com