
已知抛物线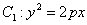 上一点
上一点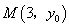 到其焦点
到其焦点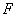 的距离为4;椭圆
的距离为4;椭圆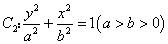 的离心率
的离心率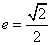 ,且过抛物线的焦点
,且过抛物线的焦点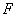 .
.
(I)求抛物线 和椭圆
和椭圆 的标准方程;
的标准方程;
(II)过点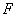 的直线
的直线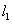 交抛物线
交抛物线 于
于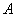 、
、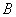 两不同点,交
两不同点,交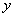 轴于点
轴于点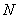 ,已知
,已知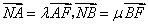 ,求证:
,求证: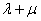 为定值.
为定值.
(III)直线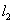 交椭圆
交椭圆 于
于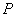 ,
,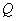 两不同点,
两不同点,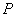 ,
,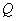 在
在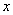 轴的射影分别为
轴的射影分别为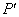 ,
,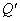 ,
,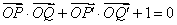 ,若点S满足:
,若点S满足: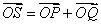 ,证明:点S在椭圆
,证明:点S在椭圆 上.
上.
科目:高中数学 来源: 题型:
设函数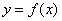 的定义域为
的定义域为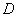 ,如果存在非零常数
,如果存在非零常数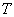 ,对于任意
,对于任意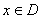 ,都有
,都有 ,则称函数
,则称函数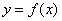 是“似周期函数”,非零常数
是“似周期函数”,非零常数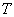 为函数
为函数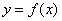 的“似周期”.现有下面四个关于“似周期函数”的命题:
的“似周期”.现有下面四个关于“似周期函数”的命题:
①如果“似周期函数”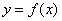 的“似周期”为-1,那么它是周期为2的周期函数;
的“似周期”为-1,那么它是周期为2的周期函数;
②函数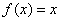 是“似周期函数”;
是“似周期函数”;
③函数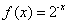 是“似周期函数”;
是“似周期函数”;
④如果函数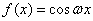 是“似周期函数”,那么“
是“似周期函数”,那么“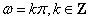 ”.
”.
其中是真命题的序号是 .(写出所有满足条件的命题序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
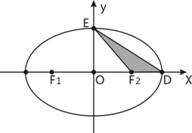
如图,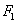 、
、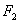 为椭圆
为椭圆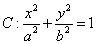 的左、右焦点,
的左、右焦点,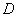 、
、 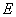 是椭圆的两个顶点,椭圆的离心率
是椭圆的两个顶点,椭圆的离心率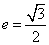 ,
,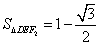 .若
.若 在椭圆
在椭圆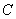 上,则点
上,则点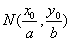 称为点
称为点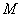 的一个“好点”.直线
的一个“好点”.直线 与椭圆交于
与椭圆交于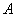 、
、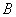 两点,
两点, 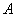 、
、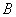 两点的“好点”分别为
两点的“好点”分别为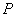 、
、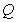 ,已知以
,已知以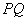 为直径的圆经过坐标原点.
为直径的圆经过坐标原点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)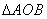 的面积是否为定值?若为定值,试求出该定值;若不为定值,请说明理由.
的面积是否为定值?若为定值,试求出该定值;若不为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
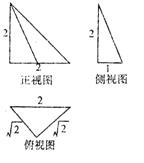
如图是一个空间几何体的三视图,该几何体的外接球的体积记为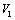 ,俯视图绕底边所在直线旋转一周形成的几何体的体积记为
,俯视图绕底边所在直线旋转一周形成的几何体的体积记为 ,则
,则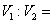 ( )
( )
(A)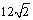 (B)
(B)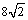 (C)
(C)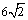 ( D)
( D)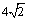
查看答案和解析>>
科目:高中数学 来源: 题型:
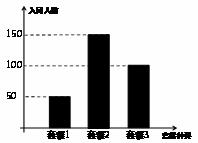
每年5月17日为国际电信日,某市电信公司在电信日当天对办理应用套餐的客户进行优惠,优惠方案如下:选择套餐一的客户可获得优惠200元,选择套餐二的客户可获得优惠500元,选择套餐三的客户可获得优惠300元电信日当天参与活动的人数统计结果如图所示,现将频率视为概率
(1) 求某人获得优惠金额不低于300元的概率;
(2) 若采用分层抽样的方式从参加活动的客户中选出6人,再从该6人中随机选出两人,求这两人获得相等优惠金额的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
函数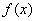 的定义域为D,若存在闭区间
的定义域为D,若存在闭区间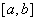
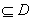 ,使得函数
,使得函数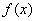 满足:
满足:
(1)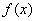 在
在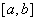 内是单调函数;(2)
内是单调函数;(2)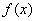 在
在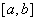 上的值域为
上的值域为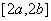 ,则称区间
,则称区间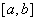 为函数
为函数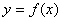 的“和谐区间”。下列函数中存在“和谐区间”的是 .
的“和谐区间”。下列函数中存在“和谐区间”的是 .
①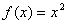 ,
,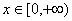 ②
②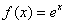 ,
,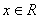
③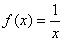 ,
,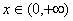 ④
④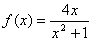 ,
,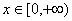
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,直三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC。若AB=AC=AA1=1,BC=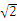 ,则异面直线A1C与B1C1所成的角为
,则异面直线A1C与B1C1所成的角为
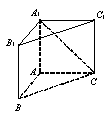
A.30° B.45° C.60° D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com