
如图,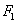 、
、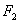 为椭圆
为椭圆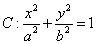 的左、右焦点,
的左、右焦点,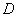 、
、 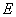 是椭圆的两个顶点,椭圆的离心率
是椭圆的两个顶点,椭圆的离心率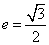 ,
,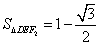 .若
.若 在椭圆
在椭圆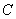 上,则点
上,则点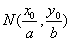 称为点
称为点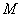 的一个“好点”.直线
的一个“好点”.直线 与椭圆交于
与椭圆交于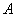 、
、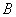 两点,
两点, 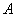 、
、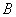 两点的“好点”分别为
两点的“好点”分别为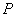 、
、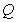 ,已知以
,已知以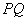 为直径的圆经过坐标原点.
为直径的圆经过坐标原点.
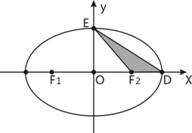
(Ⅰ)求椭圆的标准方程;
(Ⅱ)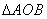 的面积是否为定值?若为定值,试求出该定值;若不为定值,请说明理由.
的面积是否为定值?若为定值,试求出该定值;若不为定值,请说明理由.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为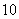 .
.
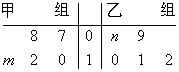
(1)分别求出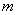 ,
,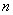 的值;
的值;
(2)分别求出甲、乙两组技工在单位时间内加工的合格零件的方差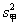 和
和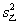 ,并由此分析两组技工的加工水平;
,并由此分析两组技工的加工水平;
(3)质检部门从该车间甲、乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,若两人加工的合格零件个数之和大于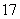 ,则称该车间“质量合格”,求该车间“质量合格”的概率.
,则称该车间“质量合格”,求该车间“质量合格”的概率.
(注:方差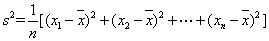 ,其中
,其中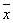 为数据
为数据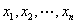 的平均数).
的平均数).
查看答案和解析>>
科目:高中数学 来源: 题型:
已知抛物线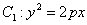 上一点
上一点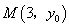 到其焦点
到其焦点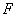 的距离为4;椭圆
的距离为4;椭圆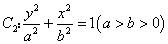 的离心率
的离心率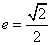 ,且过抛物线的焦点
,且过抛物线的焦点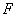 .
.
(I)求抛物线 和椭圆
和椭圆 的标准方程;
的标准方程;
(II)过点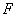 的直线
的直线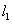 交抛物线
交抛物线 于
于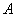 、
、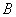 两不同点,交
两不同点,交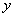 轴于点
轴于点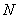 ,已知
,已知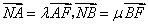 ,求证:
,求证: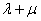 为定值.
为定值.
(III)直线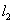 交椭圆
交椭圆 于
于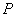 ,
,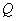 两不同点,
两不同点,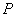 ,
,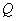 在
在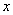 轴的射影分别为
轴的射影分别为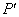 ,
,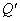 ,
,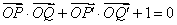 ,若点S满足:
,若点S满足: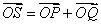 ,证明:点S在椭圆
,证明:点S在椭圆 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
非空集合 关于运算
关于运算 满足:(1)对任意的
满足:(1)对任意的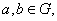 都有
都有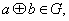 (2)存在
(2)存在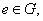 都有
都有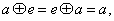 (3) 对任意的
(3) 对任意的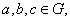 都有
都有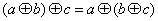 ,则称
,则称 关于运算
关于运算 为“融洽集”。现给出下列集合和运算:
为“融洽集”。现给出下列集合和运算:
①  ={非负整数},
={非负整数}, 为整数的加法。
为整数的加法。
②  ={奇数},
={奇数}, 为整数的乘法。
为整数的乘法。
③  ={平面向量}
={平面向量} 为平面向量的数量积。
为平面向量的数量积。
④ ④ ={二次三项式},
={二次三项式}, 为多项式加法。
为多项式加法。
⑤  ={虚数},
={虚数}, 为复数的乘法。其中
为复数的乘法。其中 关于运算
关于运算 为“融洽集”的是 ( )
为“融洽集”的是 ( )
A.①④⑤ B.①② C.①②③⑤ D.②③⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com