
函数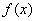 的定义域为D,若存在闭区间
的定义域为D,若存在闭区间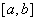
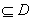 ,使得函数
,使得函数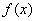 满足:
满足:
(1)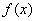 在
在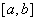 内是单调函数;(2)
内是单调函数;(2)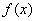 在
在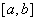 上的值域为
上的值域为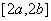 ,则称区间
,则称区间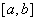 为函数
为函数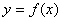 的“和谐区间”。下列函数中存在“和谐区间”的是 .
的“和谐区间”。下列函数中存在“和谐区间”的是 .
①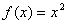 ,
,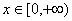 ②
②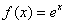 ,
,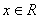
③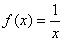 ,
,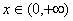 ④
④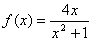 ,
,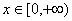
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
已知抛物线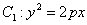 上一点
上一点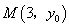 到其焦点
到其焦点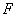 的距离为4;椭圆
的距离为4;椭圆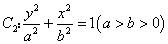 的离心率
的离心率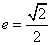 ,且过抛物线的焦点
,且过抛物线的焦点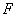 .
.
(I)求抛物线 和椭圆
和椭圆 的标准方程;
的标准方程;
(II)过点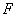 的直线
的直线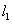 交抛物线
交抛物线 于
于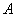 、
、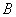 两不同点,交
两不同点,交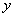 轴于点
轴于点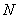 ,已知
,已知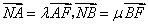 ,求证:
,求证: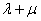 为定值.
为定值.
(III)直线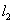 交椭圆
交椭圆 于
于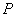 ,
,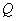 两不同点,
两不同点,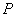 ,
,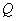 在
在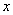 轴的射影分别为
轴的射影分别为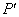 ,
,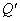 ,
,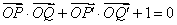 ,若点S满足:
,若点S满足: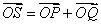 ,证明:点S在椭圆
,证明:点S在椭圆 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
非空集合 关于运算
关于运算 满足:(1)对任意的
满足:(1)对任意的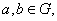 都有
都有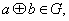 (2)存在
(2)存在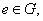 都有
都有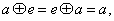 (3) 对任意的
(3) 对任意的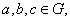 都有
都有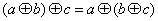 ,则称
,则称 关于运算
关于运算 为“融洽集”。现给出下列集合和运算:
为“融洽集”。现给出下列集合和运算:
①  ={非负整数},
={非负整数}, 为整数的加法。
为整数的加法。
②  ={奇数},
={奇数}, 为整数的乘法。
为整数的乘法。
③  ={平面向量}
={平面向量} 为平面向量的数量积。
为平面向量的数量积。
④ ④ ={二次三项式},
={二次三项式}, 为多项式加法。
为多项式加法。
⑤  ={虚数},
={虚数}, 为复数的乘法。其中
为复数的乘法。其中 关于运算
关于运算 为“融洽集”的是 ( )
为“融洽集”的是 ( )
A.①④⑤ B.①② C.①②③⑤ D.②③⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数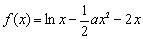 (
(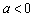 ).
).
(Ⅰ)若函数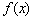 在定义域内单调递增,求实数
在定义域内单调递增,求实数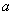 的取值范围;
的取值范围;
(Ⅱ)若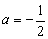 ,且关于
,且关于 的方程
的方程 在
在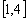 上恰有两个不等的实根,
上恰有两个不等的实根,
求实数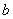 的取值范围;
的取值范围;
(Ⅲ)设各项为正数的数列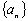 满足
满足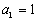 ,
,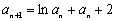 (
(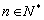 ),
),
求证: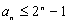 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
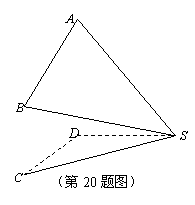
如图,在几何体SABCD中,AD⊥平面SCD,BC⊥
平面SCD,AD=DC=2,BC=1,又SD=2,∠SDC=120°.
(1)求SC与平面SAB所成角的正弦值;
(2)求平面SAD与平面SAB所成的锐二面角的余弦值.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com