
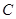 的方程为
的方程为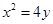 ,
,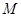 为直线
为直线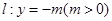 上任意一点,过点
上任意一点,过点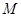 作抛物线
作抛物线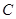 的两条切线
的两条切线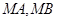 ,切点分别为
,切点分别为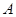 ,
,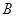 .
.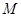 的坐标为
的坐标为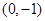 时,求过
时,求过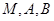 三点的圆的方程,并判断直线
三点的圆的方程,并判断直线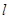 与此圆的位置关系;
与此圆的位置关系; 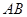 恒过定点;
恒过定点;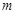 变化时,试探究直线
变化时,试探究直线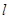 上是否存在点
上是否存在点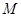 ,使
,使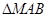 为直角三角形,若存在,有几个这样的点,若不存在,说明理由.
为直角三角形,若存在,有几个这样的点,若不存在,说明理由.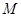 的坐标为
的坐标为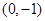 时,设过
时,设过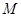 点的切线方程为
点的切线方程为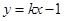 ,代入
,代入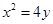 ,整理得
,整理得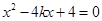 ,
,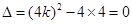 ,解得
,解得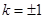 ,
,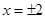 ,故得
,故得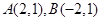 , .................2分
, .................2分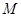 到
到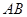 的中点
的中点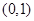 的距离为
的距离为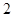 ,
,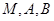 三点的圆的方程为
三点的圆的方程为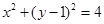 .
. 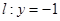 相切. ..................4分
相切. ..................4分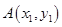 ,
,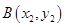 ,过抛物线上点
,过抛物线上点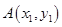 的切线方程为
的切线方程为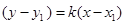 ,代入
,代入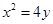 ,整理得
,整理得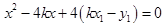
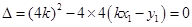 ,又因为
,又因为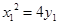 ,所以
,所以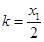 ................5分
................5分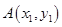 的切线方程为
的切线方程为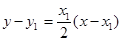 即
即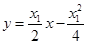
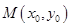 ,所以得
,所以得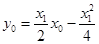 ① 即
① 即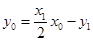
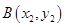 的切线为
的切线为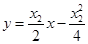 ,
,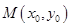 ,所以得
,所以得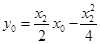 ② 即
② 即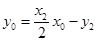 .................6分
.................6分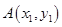 ,
,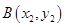 均满足
均满足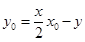 即
即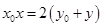 ,故直线
,故直线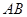 的方程为
的方程为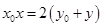 .................7分
.................7分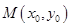 为直线
为直线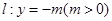 上任意一点,故
上任意一点,故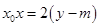 对任意
对任意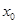 成立,所以
成立,所以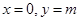 ,从而直线
,从而直线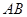 恒过定点
恒过定点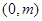 ..................8分
..................8分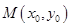 的抛物线的切线方程为
的抛物线的切线方程为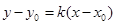
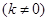 ,代入
,代入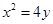 ,消去
,消去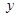 ,得
,得
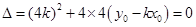 即:
即: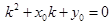 .................5分
.................5分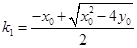 ,
,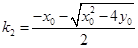 此时
此时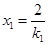 ,
,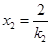
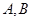 的坐标分别为
的坐标分别为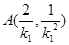 ,
,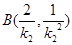 .................6分
.................6分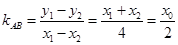 ,
,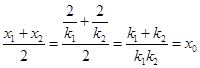 ,
,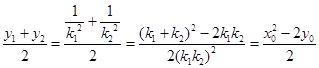 ,
,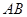 的中点坐标为
的中点坐标为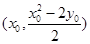
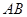 的方程为
的方程为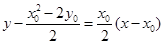 ,即
,即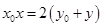 ...............7分
...............7分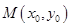 为直线
为直线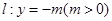 上任意一点,故
上任意一点,故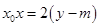 对任意
对任意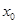 成立,所以
成立,所以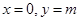 ,从而直线
,从而直线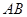 恒过定点
恒过定点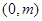 ..................8分
..................8分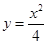 ,求导得
,求导得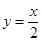 ,切点分别为
,切点分别为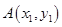 ,
,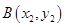 ,故过点
,故过点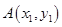 的切线斜率为
的切线斜率为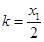 ,从而切线方程为
,从而切线方程为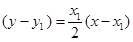 即
即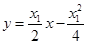
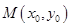 ,所以得
,所以得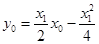 ① 即
① 即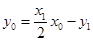
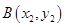 的切线为
的切线为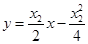 ,
,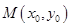 ,所以得
,所以得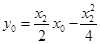 ②
② 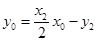 .................6分
.................6分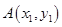 ,
,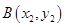 均满足
均满足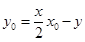 即
即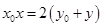 ,故直线
,故直线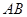 的方程为
的方程为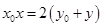 .................7分
.................7分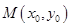 为直线
为直线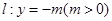 上任意一点,故
上任意一点,故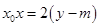 对任意
对任意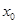 成立,所以
成立,所以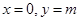 ,从而直线
,从而直线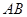 恒过定点
恒过定点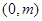 ..................8分
..................8分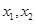 是方程
是方程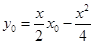 的两实根,故有
的两实根,故有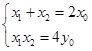
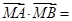
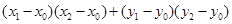
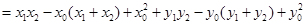 (*)
(*)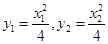 ,
,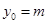 ,代入上(*)式得
,代入上(*)式得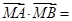
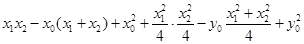
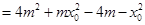
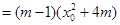 , .................9分
, .................9分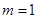 时,
时,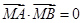 ,直线
,直线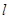 上任意一点
上任意一点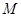 均有
均有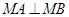 ,
,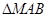 为直角三角形; .................10分
为直角三角形; .................10分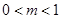 时,
时,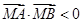 ,
,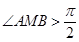 ,
,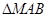 不可能为直角三角形;
不可能为直角三角形;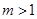 时,
时,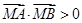 ,
,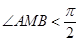 .
. 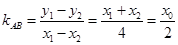 ,
,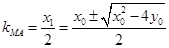 ,
,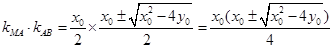
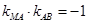 ,则
,则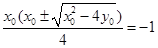 ,整理得
,整理得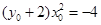 ,
,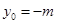 ,所以
,所以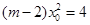 ,
,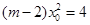 有解的充要条件是
有解的充要条件是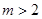 .
.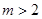 时,有
时,有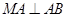 或
或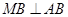 ,
,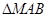 为直角三角形..............13分
为直角三角形..............13分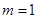 时,直线
时,直线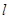 上任意一点
上任意一点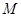 ,使
,使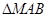 为直角三角形,当
为直角三角形,当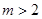 时,直线
时,直线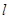 上存在两点
上存在两点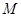 ,使
,使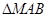 为直角三角形;当
为直角三角形;当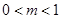 或
或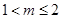 时,
时,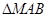 不是直角三角形.
不是直角三角形.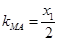 ,
,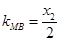 且
且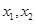 是方程
是方程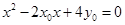 的两实根,即
的两实根,即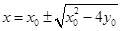 ,从而
,从而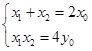 ,
,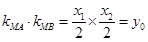
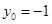 时,即
时,即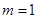 时,直线
时,直线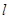 上任意一点
上任意一点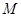 均有
均有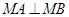 ,
,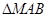 为直角三角形; .................10分
为直角三角形; .................10分 时,即
时,即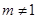 时,
时,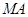 与
与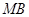 不垂直。
不垂直。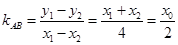 ,
,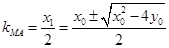 ,
,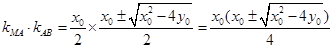
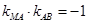 ,则
,则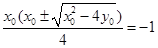 ,整理得
,整理得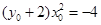 ,
,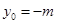 ,所以
,所以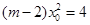 ,
,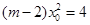 有解的充要条件是
有解的充要条件是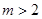 .
.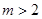 时,有
时,有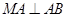 或
或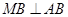 ,
,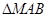 为直角三角形..............13分
为直角三角形..............13分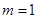 时,直线
时,直线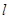 上任意一点
上任意一点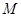 ,使
,使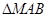 为直角三角形,当
为直角三角形,当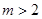 时,直线
时,直线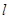 上存在两点
上存在两点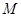 ,使
,使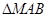 为直角三角形;当
为直角三角形;当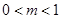 或
或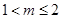 时,
时,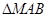 不是直角三角形.
不是直角三角形.

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
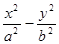 =1的一个焦点,并且这条准线与双曲线的两焦点的连线垂直,拋物线与双曲线交于点P
=1的一个焦点,并且这条准线与双曲线的两焦点的连线垂直,拋物线与双曲线交于点P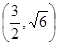 ,求拋物线方程和双曲线方程.
,求拋物线方程和双曲线方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com