
【题目】某校![]() 名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是
名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
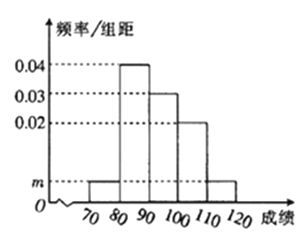
![]() 求图中
求图中![]() 的值;
的值;
![]() 根据频率分布直方图,估计这
根据频率分布直方图,估计这![]() 名学生的平均分;
名学生的平均分;
![]() 若这
若这![]() 名学生的数学成绩中,某些分数段的人数
名学生的数学成绩中,某些分数段的人数![]() 与英语成绩相应分数段的人数
与英语成绩相应分数段的人数![]() 之比如表所示,求英语成绩在
之比如表所示,求英语成绩在![]() 的人数.
的人数.
分数段 |
|
|
|
|
| 1:2 | 1:1 |
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
【题目】随着我国经济的飞速发展,人们的生活水平也同步上升,许许多多的家庭对于资金的管理都有不同的方式。最新调查表明,人们对于投资理财的兴趣逐步提高。某投资理财公司做了大量的数据调查,调查显示两种产品投资收益如下:
①投资![]() 产品的收益与投资额的算术平方根成正比;
产品的收益与投资额的算术平方根成正比;
②投资![]() 产品的收益与投资额成正比.
产品的收益与投资额成正比.
公司提供了投资1万元时两种产品的收益,分别是0.4万元和0.2万元。
(1) 分别求出![]() 产品的收益
产品的收益![]() 、
、![]() 产品的收益
产品的收益![]() 与投资额
与投资额![]() 的函数关系式;
的函数关系式;
(2) 假如现在你有10万元的资金全部用于投资理财,你该如何分配资金,才能让你的收益最大?最大收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某金店用一杆不准确的天平(两边臂不等长)称黄金,某顾客要购买![]() 黄金,售货员先将
黄金,售货员先将![]() 的砝码放在左盘,将黄金放于右盘使之平衡后给顾客;然后又将
的砝码放在左盘,将黄金放于右盘使之平衡后给顾客;然后又将![]() 的砝码放入右盘,将另一黄金放于左盘使之平衡后又给顾客,则顾客实际所得黄金( )
的砝码放入右盘,将另一黄金放于左盘使之平衡后又给顾客,则顾客实际所得黄金( )
A. 大于![]() B. 小于
B. 小于![]() C. 大于等于
C. 大于等于![]() D. 小于等于
D. 小于等于![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】20世纪30年代,里克特(C.F.Richter)制定了一种表明地震能量大小的尺度,就是使用测震仪地震能量的等级,地震能量越大,测震仪记录的地震曲线的振幅就越大,这就是我们常说的里氏震级M,其计算公式为![]() 其中,A是被测量地震的最大振幅,
其中,A是被测量地震的最大振幅,![]() 是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际的距离造成的偏差),众所周知,5级地震已经比较明显,计算8级地震的最大振幅是5级地震的最大振幅的______倍.
是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际的距离造成的偏差),众所周知,5级地震已经比较明显,计算8级地震的最大振幅是5级地震的最大振幅的______倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解学生对食堂伙食的满意程度,组织学生给食堂打分(分数为整数,满分100分),从中随机抽取一个容量为![]() 的样本,发现所有数据均在
的样本,发现所有数据均在![]() 内.现将这些分数分成以下
内.现将这些分数分成以下![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并画出了样本的频率分布直方图,部分图形如图所示.观察图形,回答下列问题:
,并画出了样本的频率分布直方图,部分图形如图所示.观察图形,回答下列问题:
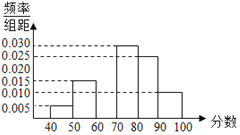
(1)算出第三组![]() 的频数,并补全频率分布直方图;
的频数,并补全频率分布直方图;
(2)请根据频率分布直方图,估计样本的众数和平均数,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某基地蔬菜大棚采用水培、无土栽培方式种植各类蔬菜.过去50周的资料显示,该地周光照量![]() (小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量
(小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量![]() (百斤)与使用某种液体肥料
(百斤)与使用某种液体肥料![]() (千克)之间对应数据为如图所示的折线图.
(千克)之间对应数据为如图所示的折线图.

(1)依据数据的折线图,是否可用线性回归模型拟合![]() 与
与![]() 的关系?请计算相关系数
的关系?请计算相关系数![]() 并加以说明(精确到0.01);(若
并加以说明(精确到0.01);(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
(2)蔬菜大棚对光照要求较大,某光照控制仪商家为该基地提供了部分光照控制仪,但每周光照控制仪最多可运行台数受周光照量![]() 限制,并有如表关系:
限制,并有如表关系:

若某台光照控制仪运行,则该台光照控制仪周利润为3000元;若某台光照控制仪未运行,则该台光照控制仪周亏损1000元.以过去50周的周光照量的频率作为周光照量发生的概率,商家欲使周总利润的均值达到最大,应安装光照控制仪多少台?
附:相关系数公式 ,参考数据
,参考数据![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】历史数据显示:某城市在每年的3月11日—3月15日的每天平均气温只可能是-5℃,-6℃,-7℃,-8℃中的一个,且等可能出现.
(Ⅰ)求该城市在3月11日—3月15日这5天中,恰好出现两次-5℃,一次-8℃的概率;
(Ⅱ)若该城市的某热饮店,随平均气温的变化所售热饮杯数如下表
平均气温t | -5℃ | -6℃ | -7℃ | -8℃ |
所售杯数y | 19 | 22 | 24 | 27 |
根据以上数据,求![]() 关于
关于![]() 的线性回归直线方程.
的线性回归直线方程.
(参考公式: ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com