解:(1)a
n=
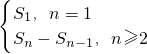
=

=2n.(2分)
(2)c
n=2nx
n-1,
T
n=2+4x+6x
2+8x
3+…+2nx
n-1,①
则xT
n=2x+4x
2+6x
3+8x
4+…+2nx
n,②
①-②,得(1-x)T
n=2+2x+2x
2+…+2x
n-1-2nx
n,
当x≠1时,(1-x)T
n=2×
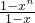
-2nx
n,
T
n=
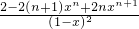
,(5分)
当x=1时,T
n=2+4+6+8+…+2n=n
2+n.(6分)
(3)当x=2时,T
n=2+(n-1)2
n+1.
则
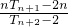
=
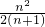
.(7分)
设f(n)=
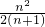
.
因为f(n+1)-f(n)=
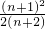
-
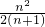
=
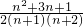
>0,(10分)
所以函数f(n)在n∈N
+上是单调增函数.(11分)
所以n=1时,f(n)取最小值

,即数列{
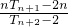
}的最小项的值为

.(12分)
分析:(1)知S
n=n
2+n,根据项与前n项和之间的关系求项与n之间的关系式,即数列{a
n}的通项公式;
(2)①由(1)知,数列{a
n}为等差数列,数列{b
n}为等差数列,c
n=a
nb
n,数列{c
n}的前n项和为T
n,用错位相减法求T
n;
②由①求出T
n,求出所要求的式子,证明这个数列的单调性,从而判定最小项.
点评:本题考查项与前n项和之间的关系,注意n=1的时候;用错位相减法求数列的前n项和,用时要观察项的特征,是否是等差数列的项与等比数列的项的乘积;求数列的最小项,要考查数列的单调性,此时把数列看作自变量为正整数集的函数.

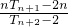 }的最小项的值.
}的最小项的值.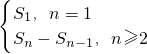 =
= =2n.(2分)
=2n.(2分)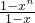 -2nxn,
-2nxn,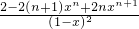 ,(5分)
,(5分)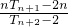 =
=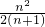 .(7分)
.(7分)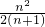 .
.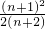 -
-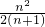 =
=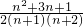 >0,(10分)
>0,(10分) ,即数列{
,即数列{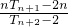 }的最小项的值为
}的最小项的值为 .(12分)
.(12分)

 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案