
设 为不小于2的正整数,对任意
为不小于2的正整数,对任意 ,若
,若 (其中
(其中 ,
, ,且
,且 ),则记
),则记 ,如
,如 ,
, .下列关于该映射
.下列关于该映射 的命题中,正确的是.
的命题中,正确的是.
①若 ,
, ,则
,则
②若 ,
, ,
, ,且
,且 ,则
,则
③若 ,
, ,
, ,
, ,且
,且 ,
, ,则
,则
④若 ,
, ,
, ,
, ,且
,且 ,
, ,则
,则 .
.
科目:高中数学 来源: 题型:填空题
一般地,如果函数 的定义域为
的定义域为 ,值域也是
,值域也是 ,则称函数
,则称函数 为“保域函数”,下列函数中是“保域函数”的有_____________.(填上所有正确答案的序号)
为“保域函数”,下列函数中是“保域函数”的有_____________.(填上所有正确答案的序号)
① ;②
;②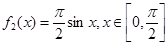 ;
;
③ ;④
;④ ;
;
⑤ .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com