
【题目】如图,在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
:![]() ,点
,点![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() (不在y轴上).
(不在y轴上).

(1)若直线![]() 的斜率为3,求
的斜率为3,求![]() 的长度;
的长度;
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证:![]() 为定值,并求出该定值;
为定值,并求出该定值;
(3)设![]() 的中点为
的中点为![]() ,是否存在直线
,是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
【答案】(1)![]() ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
【解析】
(1)求出圆心O到直线![]() 的距离,已知半径通过勾股定理即可算出弦长的一半,即可算出弦长。(2)设
的距离,已知半径通过勾股定理即可算出弦长的一半,即可算出弦长。(2)设![]() ,直线
,直线![]() 的方程为
的方程为![]() ,联立圆的方程通过韦达定理化简
,联立圆的方程通过韦达定理化简![]() 即可。(3)设点
即可。(3)设点![]() ,根据
,根据![]() ,得
,得![]() ,表示出
,表示出![]() ,
,![]() 的关系,再联立直线和圆的方程得到
的关系,再联立直线和圆的方程得到![]() ,
,![]() 与k的关系,代入可解出k,最后再通过有两个交点
与k的关系,代入可解出k,最后再通过有两个交点![]() 判断即可求出k值。
判断即可求出k值。
(1)由直线![]() 的斜率为3,可得直线
的斜率为3,可得直线![]() 的方程为
的方程为![]()
所以圆心![]() 到直线
到直线![]() 的距离为
的距离为![]()
所以
(2)直线![]() 的方程为
的方程为![]() ,
,
代入圆![]() 可得方程
可得方程![]()
设![]() ,则
,则![]()


所以![]() 为定值,定值为0
为定值,定值为0
(3)设点![]() ,由
,由![]() ,可得:
,可得:![]() ,即
,即
![]() ,化得:
,化得:![]()
由(*)及直线![]() 的方程可得:
的方程可得: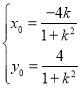 ,代入上式可得:
,代入上式可得:
 ,可化为:
,可化为:![]()
求得:![]()
又由(*)![]() 解得:
解得:![]()
所以![]() 不符合题意,所以不存在符合条件的直线
不符合题意,所以不存在符合条件的直线![]() .
.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】将3本相同的小说,2本相同的诗集全部分给4名同学,每名同学至少1本,则不同的分法有( )
A. 24种 B. 28种 C. 32种 D. 36种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二项式![]() 的二项式系数和为256.
的二项式系数和为256.
(1)求展开式中二项式系数最大的项;
(2)求展开式中各项的系数和;
(3)展开式中是否有有理项,若有,求系数;若没有,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x﹣alnx+ ![]() .
.
(Ⅰ)若a>1,求函数f(x)的单调区间;
(Ⅱ)若a>3,函数g(x)=a2x2+3,若存在x1 , x2∈[ ![]() ,2],使得|f(x1)﹣g(x2)|<9成立,求a的取值范围.
,2],使得|f(x1)﹣g(x2)|<9成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() 底面
底面![]() ,
, ![]() 是棱
是棱![]() 的中点,
的中点,
且![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)如果![]() 是棱
是棱![]() 上一点,且直线
上一点,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某百货公司1~6月份的销售量![]() 与利润
与利润![]() 的统计数据如下表:
的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售量x(万件) | 10 | 11 | 13 | 12 | 8 | 6 |
利润y(万元) | 22 | 25 | 29 | 26 | 16 | 12 |
附:
(1)根据2~5月份的统计数据,求出![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]()
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过![]() 万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?(参考公式:,
万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?(参考公式:,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD为梯形,AD∥BC,BC=6,PA=AD=CD=2,E为BC上一点且BE= ![]() BC,PB⊥AE.
BC,PB⊥AE. 
(1)求证:AB⊥PE;
(2)求二面角B﹣PC﹣D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com