
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}-1$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{1}{2}$ |
分析 由实数x,y满足:|x|≤y≤1,可得可行域为:P(1,0),Q点为可行域内的任意一点,当PQ⊥直线y=x时,|PQ|取得最小值,因此|PQ|2取得最小值.
解答 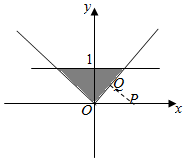 解:由实数x,y满足:|x|≤y≤1,可得可行域为:
解:由实数x,y满足:|x|≤y≤1,可得可行域为:
P(1,0),Q点为可行域内的任意一点,当PQ⊥直线y=x时,
|PQ|取得最小值,因此|PQ|2取得最小值,
则x2+y2-2x=(x-1)2+y2-1≥|PQ|2-1=$(\frac{1-0}{\sqrt{2}})^{2}$-1=-$\frac{1}{2}$.
∴x2+y2-2x的最小值为-$\frac{1}{2}$.
故选:D.
点评 本题考查了线性规划有关知识、点到直线的距离公式、数形结合思想方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知△ABC满足$AB=4,AC=2,∠BAC=\frac{2π}{3}$,点D、E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则 $\overrightarrow{AF}•\overrightarrow{DC}$的值为( )
已知△ABC满足$AB=4,AC=2,∠BAC=\frac{2π}{3}$,点D、E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则 $\overrightarrow{AF}•\overrightarrow{DC}$的值为( )| A. | -$\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | -2 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,若N=10,则输出的数等于( )
如图,若N=10,则输出的数等于( )| A. | $\frac{10}{9}$ | B. | $\frac{9}{10}$ | C. | $\frac{10}{11}$ | D. | $\frac{12}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 指标 | 1号小白鼠 | 2号小白鼠 | 3号小白鼠 | 4号小白鼠 | 5号小白鼠 |
| A | 5 | 7 | 6 | 9 | 8 |
| B | 2 | 2 | 3 | 4 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 3 | 4 | 5 | 6 | 7 | 8 | |
| y | 4.0 | 2.5 | -0.5 | 0.5 | -2.0 | -3.0 |
| A. | ${\;}_{a}^{∧}$>0,${\;}_{b}^{∧}$>0 | B. | ${\;}_{a}^{∧}$>0,${\;}_{b}^{∧}$<0 | C. | ${\;}_{a}^{∧}$<0,${\;}_{b}^{∧}$>0 | D. | ${\;}_{a}^{∧}$<0,${\;}_{b}^{∧}$<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com