
分析 首先利用均值不等式,得到x2+y2+z2≥xy+xz+yz,进而根据不等式的基本性质,得到答案.
解答 解:∵(x-y)2+(x-z)2+(y-z)2≥0,
∴2(x2+y2+z2)≥2(xy+xz+yz),
∴x2+y2+z2≥xy+xz+yz,
∴$\frac{xy+yz+zx}{{x}^{2}+{y}^{2}+{z}^{2}}$≤1,
∴$\frac{xy+yz+zx}{6{x}^{2}+6{y}^{2}+6{z}^{2}}$≤$\frac{1}{6}$,
故$\frac{xy+yz+zx}{6{x}^{2}+6{y}^{2}+6{z}^{2}}$的最大值是$\frac{1}{6}$
故答案为:$\frac{1}{6}$
点评 本题主要考查了基本不等式的应用.基本不等式是解决多项式和函数的最值问题的常用方法,平时应熟练掌握.


科目:高中数学 来源: 题型:填空题
| 房间A | 房间B | 房间C |
| 35m2 | 20m2 | 28m2 |
| 涂料1 | 涂料2 | 涂料3 |
| 16元/m2 | 18元/m2 | 20元/m2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60 | B. | 36 | C. | -24 | D. | -60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
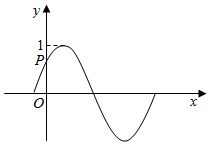
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{6}$或$\frac{5π}{6}$ | D. | -$\frac{π}{6}$或$\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com