练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    一个空间几何体的三视图如图所示，则该几何体的表面积为__________．


    50(1＋)　

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    某高级中学共有学生3 000名，各年级男、女生人数如下表：

    高一年级

    高二年级

    高三年级

    女生

    523

    x

    y

    男生

    487

    490

    z

    已知在全校学生中随机抽取1名，抽到高二年级女生的概率是0.17.若现需对各年级用分层抽样的方法在全校抽取300名学生，则应在高三年级抽取的学生人数为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设A是整数集的一个非空子集，对于k∈A，如果k－1∉A且k＋1∉A，那么称k是集合A的一个“好元素”．给定集合S＝{1,2,3,4,5,6,7,8}，由S的3个元素构成的所有集合中，不含“好元素”的集合共有________个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    给出下列四个结论：

    ①命题“∃x∈R，x2－x＞0”的否定是“∀x∈R，x2－x≤0”；

    ②函数f(x)＝x－sin x(x∈R)有3个零点；

    ③对于任意实数x，有f(－x)＝－f(x)，g(－x)＝g(x)，且x＞0时，f′(x)＞0，g′(x)＞0，则x＜0时，f′(x)＞g′(x)．

    其中正确结论的序号是________．(请写出所有正确结论的序号)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


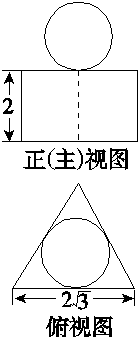
    一个几何体的正(主)视图和俯视图如图所示，其中俯视图是边长为2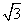的正三角形，且圆与三角形内切，则侧(左)视图的面积为(　　)

    A．6＋π                                B．4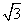＋π

    C．6＋4π                               D．4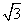＋4π

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知一个三棱柱，其底面是正三角形，且侧棱与底面垂直，一个体积为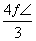的球体与棱柱的所有面均相切，那么这个三棱柱的表面积是(　　)

    A．6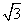                                 B．12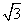 

    C．18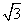                                D．24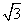

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如果一个棱锥的底面是正多边形，并且顶点在底面的射影是底面的中心，这样的棱锥叫做正棱锥．已知一个正六棱锥的各个顶点都在半径为3的球面上，则该正六棱锥的体积的最大值为______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知等比数列{an}满足an＋1＋an＝9·2n－1，n∈N*.

    (1)求数列{an}的通项公式；

    (2)设数列{an}的前n项和为Sn，若不等式Sn＞kan－2对一切n∈N*恒成立，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示，平行四边形OABC，顶点O、A、C分别表示0、3＋2i、－2＋4i，试求：

    (1) 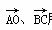所表示的复数；

    (2) 对角线所表示的复数；

    (3) 求B点对应的复数．

    查看答案和解析>>

    同步练习册答案