
如图,在边长为1的正方形OABC内取一点P(x,y),求: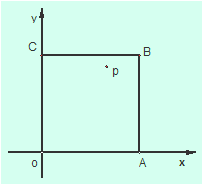
(1)点P到原点距离小于1的概率;
(2)以x,y,1为边长能构成三角形的概率;
(3)以x,y,1为边长能构成锐角三角形的概率
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
中央电视台星光大道某期节目中,有5位实力均等的选手参加比赛,经过四轮比赛决出周冠军(每一轮比赛淘汰l位选手).
(1)求甲、乙两位选手都进入第三轮比赛的概率;
(2)求甲选手在第三轮被淘汰的的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人在罚球线互不影响地投球,命中的概率分别为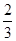 与
与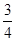 ,投中得1分,投不中得0分.
,投中得1分,投不中得0分.
(1)甲、乙两人在罚球线各投球一次,求两人得分之和 的数学期望;
的数学期望;
(2)甲、乙两人在罚球线各投球二次,求甲恰好比乙多得分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲有一个箱子,里面放有x个红球,y个白球(x,y≥0,且x+y=4);乙有一个箱子,里面放有2个红球,1个白球,1个黄球.现在甲从箱子里任取2个球,乙从箱子里任取1个球.若取出的3个球颜色全不相同,则甲获胜.
(1)试问甲如何安排箱子里两种颜色球的个数,才能使自己获胜的概率最大?
(2)在(1)的条件下,求取出的3个球中红球个数的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
从编号为1,2,3,4,5的五个形状大小相同的球中,任取2个球,求:(1)取到的这2个球编号之和为5的概率;(2)取到的这2个球编号之和为奇数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人独立地破译1个密码, 他们能译出密码的概率分别为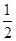 和
和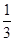 , 求:
, 求:
(1)甲、乙两人至少有一个人破译出密码的概率;
(2)两人都没有破译出密码的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个袋中装有大小相同的黑球和白球共9个,从中任取3个球,记随机变量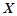 为取出3球中白球的个数,已知
为取出3球中白球的个数,已知 .
.
(Ⅰ)求袋中白球的个数;
(Ⅱ)求随机变量 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)电信公司进行促销活动,促销方案为顾客消费1000元,便可获得奖券一张,每张奖券中奖的概率为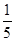 ,中奖后电信公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为X(元).
,中奖后电信公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为X(元).
(I)求X的分布列;(II)试说明小李出资50元增加1张奖券是否划算。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com