
【题目】从2016年1月1日起,广东、湖北等18个保监局所辖地区将纳入商业车险改革试点范围,其中最大的变化是上一年的出险次数决定了下一年的保费倍率,具体关系如表:
上一年的 | 0 | 1 | 2 | 3 | 4 | 5次以上(含5次) |
下一年 | 85% | 100% | 125% | 150% | 175% | 200% |
连续两年没有出险打7折,连续三年没有出险打6折 | ||||||
有评估机构从以往购买了车险的车辆中随机抽取1000辆调查,得到一年中出险次数的频数分布如下(并用相应频率估计车辆每年出险次数的概率):
一年中出险次数 | 0 | 1 | 2 | 3 | 4 | 5次以上(含5次) |
频数 | 500 | 380 | 100 | 15 | 4 | 1 |
(1)求某车在两年中出险次数不超过2次的概率;
(2)经验表明新车商业车险保费与购车价格有较强的线性相关关系,估计其回归直线方程为: ![]() =120x+1600.(其中x(万元)表示购车价格,y(元)表示商业车险保费).李先生2016 年1月购买一辆价值20万元的新车.根据以上信息,试估计该车辆在2017 年1月续保时应缴交的保费,并分析车险新政是否总体上减轻了车主负担.(假设车辆下一年与上一年都购买相同的商业车险产品进行续保)
=120x+1600.(其中x(万元)表示购车价格,y(元)表示商业车险保费).李先生2016 年1月购买一辆价值20万元的新车.根据以上信息,试估计该车辆在2017 年1月续保时应缴交的保费,并分析车险新政是否总体上减轻了车主负担.(假设车辆下一年与上一年都购买相同的商业车险产品进行续保)
【答案】
(1)解:设某车在两年中出险次数为N,则P(N≤2)=P(N=0)+P(N=1)+P(N=2)= ![]() ×
× ![]() +C21×
+C21× ![]() ×
× ![]() +
+ ![]() ×
× ![]() =0.8477
=0.8477
∴某车在两年中出险次数不超过2次的概率为0.8744;
(2)解:设该车辆2017年的保费倍率为X,则X为随机变量,X的取值为0.85,1,1.25,1.5,1.75,2
X的分布列为)X的分布列为:
X | 0.85 | 1 | 1.25 | 1.5 | 1.75 | 2 |
P | 0.5 | 0.38 | 0.1 | 0.015 | 0.004 | 0.001 |
计算得下一年的保费倍率的数学期望E(X)=0.85×0.5+1×0.38+1.25×0.1+1.5×0.015+1.75×0.004+2×0.001=0.9615.
该车辆估计2017年应缴保费为:(120×20+1600)×0.9615=3846元,
∵0.9615<1,
∴车险新政总体上减轻了车主负担.
【解析】(1)根据互斥事件的概率公式计算即可;(2)求出下一年车险倍率X的分布列,计算X的数学期望,得出车主下一年的保费,根据X的数学期望是否大于1得出结论.


科目:高中数学 来源: 题型:
【题目】如图,已知AD、BE、CF分别是△ABC三边的高,H是垂心,AD的延长线交△ABC的外接圆于点G. 
(1)求证:∠CHG=∠ABC;
(2)求证:ABGD=ADHC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是实数,
是实数,![]() ,
,
(1)若函数![]() 为奇函数,求
为奇函数,求![]() 的值;
的值;
(2)试用定义证明:对于任意![]() ,
,![]() 在
在![]() 上为单调递增函数;
上为单调递增函数;
(3)若函数![]() 为奇函数,且不等式
为奇函数,且不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某地高一学生的体能状况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组频数为12.
(1)第二小组的频率是多少?样本容量是多少?
(2)若次数在110以上为达标,试估计全体高一学生的达标率为多少?
(3)通过该统计图,可以估计该地学生跳绳次数的众数是______,中位数是_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
组 别 | 频数 | 频率 |
[145.5,149.5) | 1 | 0.02 |
[149.5,153.5) | 4 | 0.08 |
[153.5,157.5) | 20 | 0.40 |
[157.5,161.5) | 15 | 0.30 |
[161.5,165.5) | 8 | 0.16 |
[165.5,169.5) | m | n |
合 计 | M | N |

(1)求出表中![]() 所表示的数;
所表示的数;
(2)画出频率分布直方图;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mx2+(1-3m)x-4,m∈R.
(1)当m=1时,求f(x)在区间[-2,2]上的最大值和最小值.
(2)解关于x的不等式f(x)>-1.
(3)当m<0时,若存在x0∈(1,+∞),使得f(x)>0,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展《中国汉字听写大会》的活动.为响应学校号召,2(9)班组建了兴趣班,根据甲、乙两人近期8次成绩画出茎叶图,如图所示,甲的成绩中有一个数的个位数字模糊,在茎叶图中用![]() 表示.(把频率当作概率).
表示.(把频率当作概率).
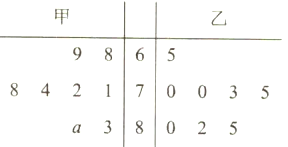
(1)假设![]() ,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
(2)假设数字![]() 的取值是随机的,求乙的平均分高于甲的平均分的概率.
的取值是随机的,求乙的平均分高于甲的平均分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题:
①已知-1<a<b<0,则0.3a>a2>ab;
②若正实数a、b满足a+b=1,则ab有最大值![]() ;
;
③若正实数a、b满足a+b=1,则![]() 有最大值
有最大值![]() ;
;
④x,y∈(0,+∞),x3+y3>x2y+xy2.
其中真命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+log2x+b在区间( ![]() ,4)上有零点,则实数b的取值范围是( )
,4)上有零点,则实数b的取值范围是( )
A.(﹣10,0)
B.(﹣8,1)
C.(0,10)
D.(1,12)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com