
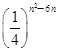 (n∈N*),bn=log2an,则数列{bn}的前n项和Sn取最大时,n=________.
(n∈N*),bn=log2an,则数列{bn}的前n项和Sn取最大时,n=________. 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源:不详 题型:填空题
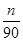 (21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是________.
(21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是________.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
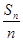 ,证明数列{bn}是等差数列,并求其前n项和Tn.
,证明数列{bn}是等差数列,并求其前n项和Tn.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
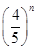 Sn,是否存在正整数m,对一切正整数n,总有Tn≤Tm?若存在,求m的值;若不存在,说明理由.
Sn,是否存在正整数m,对一切正整数n,总有Tn≤Tm?若存在,求m的值;若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com