
 (2)当1<n<k时,an<bn;当n>k时,an>bn;当n=1,k时,an=bn.
(2)当1<n<k时,an<bn;当n>k时,an>bn;当n=1,k时,an=bn.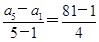 =20,
=20,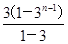 -(20n-19)·3n=(29-20n)·3n-29,所以Sn=
-(20n-19)·3n=(29-20n)·3n-29,所以Sn= .(7分)
.(7分)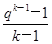 ,
,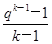 .又bn=qn-1,(9分)所以bn-an=qn-1-
.又bn=qn-1,(9分)所以bn-an=qn-1-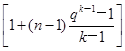
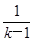 [(k-1)(qn-1-1)-(n-1)(qk-1-1)]
[(k-1)(qn-1-1)-(n-1)(qk-1-1)]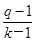 [(k-1)(qn-2+qn-3+…+q+1)-(n-1)(qk-2+qk-3+…+q+1)].(11分)
[(k-1)(qn-2+qn-3+…+q+1)-(n-1)(qk-2+qk-3+…+q+1)].(11分)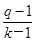 [(k-n)(qn-2+qn-3+…+q+1)-(n-1)(qk-2+qk-3+…+qn-1)]
[(k-n)(qn-2+qn-3+…+q+1)-(n-1)(qk-2+qk-3+…+qn-1)]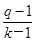 [(k-n)(n-1)qn-2-(n-1)(k-n)qn-1]=-
[(k-n)(n-1)qn-2-(n-1)(k-n)qn-1]=-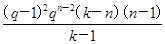
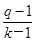 [(k-1)(qn-2+qn-3+…+qk-1)-(n-k)(qk-2+qk-3+…+q+1)]
[(k-1)(qn-2+qn-3+…+qk-1)-(n-k)(qk-2+qk-3+…+q+1)]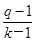 [(k-1)(n-k)qk-1-(n-k)(k-1)qk-2]
[(k-1)(n-k)qk-1-(n-k)(k-1)qk-2]

科目:高中数学 来源:不详 题型:解答题
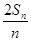 =an+1-
=an+1-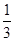 n2-n-
n2-n-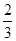 ,n∈N*.
,n∈N*.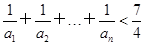 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
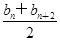 ≤bn+1(n∈N*);②bn≤M(n∈N*,M是与n无关的常数)的无穷数列{bn}叫“特界” 数列.
≤bn+1(n∈N*);②bn≤M(n∈N*,M是与n无关的常数)的无穷数列{bn}叫“特界” 数列.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 1 | | 2 | | |
| 0.5 | | 1 | | |
| | | a | | |
| | | | b | |
| | | | | c |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
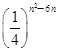 (n∈N*),bn=log2an,则数列{bn}的前n项和Sn取最大时,n=________.
(n∈N*),bn=log2an,则数列{bn}的前n项和Sn取最大时,n=________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com