
 为平面内两定点,过该平面内动点
为平面内两定点,过该平面内动点 作直线
作直线 的垂线,垂足为
的垂线,垂足为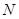 .若
.若 ,其中
,其中 为常数,则动点
为常数,则动点 的轨迹不可能是( )
的轨迹不可能是( )| A.圆 | B.椭圆 | C.抛物线 | D.双曲线 |
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:高中数学 来源:不详 题型:解答题
 :
: 的准线与
的准线与 轴交于点
轴交于点 ,焦点为
,焦点为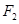 ;椭圆
;椭圆 以
以 和
和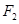 为焦点,离心率
为焦点,离心率 .设
.设 是
是 与
与 的一个交点.
的一个交点.
 的方程.
的方程. 过
过 的右焦点
的右焦点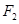 ,交
,交 于
于 两点,且
两点,且 等于
等于 的周长,求
的周长,求 的方程.
的方程.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
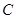 的离心率
的离心率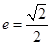 ,长轴的左右端点分别为
,长轴的左右端点分别为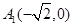 ,
,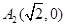 .
.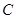 的方程;
的方程;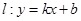 与曲线
与曲线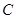 有且只有一个公共点
有且只有一个公共点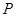 ,且与直线
,且与直线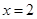 相交于点
相交于点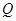 .
.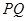 为直径的圆过定点
为直径的圆过定点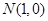 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 上的动点,点D是P在
上的动点,点D是P在 轴上投影,M为PD上一点,且
轴上投影,M为PD上一点,且 .
.
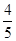 的直线被C所截线段的长度.
的直线被C所截线段的长度.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 轴上,A是右顶点,B是虚轴的上端点,F是左焦点,
轴上,A是右顶点,B是虚轴的上端点,F是左焦点, ,类比“黄金双曲线”,推算出“黄金椭圆”(如图)的离心率
,类比“黄金双曲线”,推算出“黄金椭圆”(如图)的离心率 =_________;
=_________;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com