
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是菱形, ![]() ,PD⊥平面ABCD,PD=AD=3,PM=2MD,AN=2NB,E是AB中点.
,PD⊥平面ABCD,PD=AD=3,PM=2MD,AN=2NB,E是AB中点.
(Ⅰ)求证:直线AM∥平面PNC;
(Ⅱ)求证:直线CD⊥平面PDE;
(III)在AB上是否存在一点G,使得二面角G﹣PD﹣A的大小为 ![]() ,若存在,确定G的位置,若不存在,说明理由.
,若存在,确定G的位置,若不存在,说明理由.
【答案】证明:(Ⅰ)在PC上取一点F,使PF=2FC,连接MF,NF,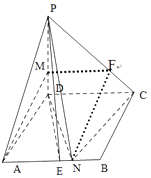
∵PM=2MD,AN=2NB,
∴MF∥DC,MF= ![]() ,AN∥DC,AN=
,AN∥DC,AN= ![]() .
.
∴MF∥AN,MF=AN,
∴MFNA为平行四边形,
即AM∥NA.
又AM平面PNC,
∴直线AM∥平面PNC;
(Ⅱ)∵E是AB中点,底面ABCD是菱形,∠DAB=60°,∴∠AED=90°.
∵AB∥CD,∴∠EDC=90°,即CD⊥DE.
又PD⊥平面ABCD,∴CD⊥PD.
又DE∩PD=D,∴直线CD⊥平面PDE;
(III)由(Ⅱ)可知DP,DE,DC,相互垂直,以D为原点,如图建立空间直角坐标系.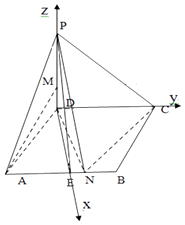
则 ![]() .
.
设面PDA的法向量 ![]() ,
,
由 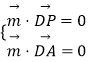 ,得
,得 ![]() .
.
设面PDG的法向量 ![]() ,
,
由  ,得
,得 ![]() .
.
∴cos60°= 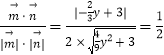 .
.
解得 ![]() ,则
,则 ![]() .
.
∴G与B重合.点B的位置为所求.
【解析】(Ⅰ)在PC上取一点F,使PF=2FC,连接MF,NF,结合已知可得MF∥DC,MF= ![]() ,AN∥DC,AN=
,AN∥DC,AN= ![]() .从而可得MFNA为平行四边形,即AM∥NA.再由线面平行的判定可得直线AM∥平面PNC;(Ⅱ)由E是AB中点,底面ABCD是菱形,∠DAB=60°,得∠AED=90°.进一步得到CD⊥DE.再由PD⊥平面ABCD得CD⊥PD.由线面垂直的判定可得直线CD⊥平面PDE;(III)由(Ⅱ)可知DP,DE,DC,相互垂直,以D为原点,建立空间直角坐标系.然后利用平面法向量所成角的余弦值求得G点位置.
.从而可得MFNA为平行四边形,即AM∥NA.再由线面平行的判定可得直线AM∥平面PNC;(Ⅱ)由E是AB中点,底面ABCD是菱形,∠DAB=60°,得∠AED=90°.进一步得到CD⊥DE.再由PD⊥平面ABCD得CD⊥PD.由线面垂直的判定可得直线CD⊥平面PDE;(III)由(Ⅱ)可知DP,DE,DC,相互垂直,以D为原点,建立空间直角坐标系.然后利用平面法向量所成角的余弦值求得G点位置.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对直线与平面垂直的判定的理解,了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)是定义在R上的奇函数,且f(x﹣1)为偶函数,当x∈[0,1]时, ![]() ,若函数g(x)=f(x)﹣x﹣b恰有一个零点,则实数b的取值集合是( )
,若函数g(x)=f(x)﹣x﹣b恰有一个零点,则实数b的取值集合是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1的极坐标方程为ρcosθ﹣ρsinθ+2=0,曲线C2的参数方程为 ![]() (α为参数),将曲线C2上的所有点的横坐标变为原来的3倍,纵坐标变为原来的
(α为参数),将曲线C2上的所有点的横坐标变为原来的3倍,纵坐标变为原来的 ![]() 倍,得到曲线C3 .
倍,得到曲线C3 .
(1)写出曲线C1的参数方程和曲线C3的普通方程;
(2)已知点P(0,2),曲线C1与曲线C3相交于A,B,求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.y=sinx的图象向右平移![]() 个单位得y=cosx的图象
个单位得y=cosx的图象
B.y=cosx的图象向右平移![]() 个单位得y=sinx的图象
个单位得y=sinx的图象
C.当φ>0时,y=sinx的图象向右平移φ个单位可得y=sin(x+φ)的图象
D.当φ<0时,y=sinx的图象向左平移φ个单位可得y=sin(x﹣φ)的图象
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx+cosx,x∈R.
(1)求函数f(x)的最小正周期和最大值;
(2)函数y=f(x)的图象可由y=sinx的图象经过怎么的变换得到?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x1 , x2是方程e﹣x+2=|lnx|的两个解,则( )
A.0<x1x2< ![]()
B.![]() <x1x2<1
<x1x2<1
C.1<x1x2<e
D.x1x2>e
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
设f(x)=|ax﹣1|.
(Ⅰ)若f(x)≤2的解集为[﹣6,2],求实数a的值;
(Ⅱ)当a=2时,若存在x∈R,使得不等式f(2x+1)﹣f(x﹣1)≤7﹣3m成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑. 如图,在阳马P﹣ABCD中,侧棱PD⊥底面ABCD,且PD=CD,E为PC中点,点F在PB上,且PB⊥平面DEF,连接BD,BE.
(Ⅰ)证明:DE⊥平面PBC;
(Ⅱ)试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
(Ⅲ)已知AD=2, ![]() ,求二面角F﹣AD﹣B的余弦值.
,求二面角F﹣AD﹣B的余弦值.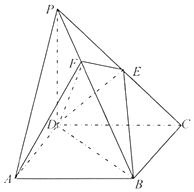
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某成衣批发店为了对一款成衣进行合理定价,将该款成衣按事先拟定的价格进行试销,得到了如下数据:
批发单价x(元) | 80 | 82 | 84 | 86 | 88 | 90 |
销售量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程 ![]() ,其中
,其中 ![]()
(2)预测批发单价定为85元时,销售量大概是多少件?
(3)假设在今后的销售中,销售量与批发单价仍然服从(1)中的关系,且该款成衣的成本价为40元/件,为使该成衣批发店在该款成衣上获得更大利润,该款成衣单价大约定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com