
分析 (1)求得导数,由极值点的定义可得x1,x2为x2+(a+2)x+a=0的两根,运用韦达定理和求根公式,以及导数的几何意义,即可得到所求值;
(2)运用分析法证明,要证不等式成立,即证(x-2)ex-m+1>$\frac{3}{4}$•$\frac{1}{{x}^{2}+\sqrt{5}x+2}$,主要求得左边函数的最小值不小于右边函数的最大值,运用导数和二次函数的最值求法,即可得证.
解答 解:(1)函数f(x)=(x2+ax)ex的导数为
f′(x)=(x2+(a+2)x+a)ex,
由题意可得x1,x2为x2+(a+2)x+a=0的两根,
x1+x2=-a-2=-2-$\sqrt{5}$,解得a=$\sqrt{5}$,
即有x1x2=$\sqrt{5}$,
解得x1=$\frac{-5-\sqrt{5}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$,
y=f(x)在点(0,f(0))处的切线的斜率为k=a=$\sqrt{5}$,
综上可得,k=$\sqrt{5}$,x1=$\frac{-5-\sqrt{5}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$;
(2)证明:要证[f(x)+2ex]•[(x-2)ex-m+1]>$\frac{3}{4}$ex,
即证(x2+$\sqrt{5}$x+2)•[(x-2)ex-m+1]>$\frac{3}{4}$,
即证(x-2)ex-m+1>$\frac{3}{4}$•$\frac{1}{{x}^{2}+\sqrt{5}x+2}$,
由y=(x-2)ex-m+1的导数为(x-1)ex,
当x>1时,函数递增,当x<1时,函数递减.
即有x=1处取得最小值,且为1-m-e;
又$\frac{3}{4}$•$\frac{1}{{x}^{2}+\sqrt{5}x+2}$≤$\frac{3}{4}$•$\frac{1}{2-\frac{5}{4}}$=1,
当m≤-e时,1-m-e≥1+e-e=1,
则(x-2)ex-m+1>$\frac{3}{4}$•$\frac{1}{{x}^{2}+\sqrt{5}x+2}$成立,
故原不等式成立.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查韦达定理及求根公式,以及不等式的证明,注意转化为函数的最值的比较,属于中档题.


科目:高中数学 来源: 题型:解答题
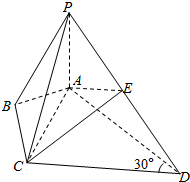 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
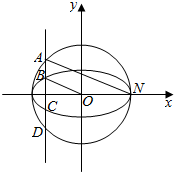 如图,已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的半焦距为c,原点O到经过两点(c、0),(0,b)的直线的距离为λc(λ∈(0,1),垂直于x轴的直线l与椭圆C1及圆C2:x2+y2=a2均有两个交点,这四个交点按其坐标从大到小分别为A、B、C、D
如图,已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的半焦距为c,原点O到经过两点(c、0),(0,b)的直线的距离为λc(λ∈(0,1),垂直于x轴的直线l与椭圆C1及圆C2:x2+y2=a2均有两个交点,这四个交点按其坐标从大到小分别为A、B、C、D查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -12 | B. | -20 | C. | 12 | D. | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com