
分析 由题意和距离公式分别可得三角形的三边,由余弦定理可得.
解答 解:∵△ABC的顶点为A(1,3),B(-1,2)和C(4,1),
∴a=BC=$\sqrt{(-1-4)^{2}+(2-1)^{2}}$=$\sqrt{26}$,
b=AC=$\sqrt{(1-4)^{2}+(3-1)^{2}}$=$\sqrt{13}$,
c=AB=$\sqrt{(-1-1)^{2}+(2-3)^{2}}$=$\sqrt{5}$,
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{35\sqrt{2}}{52}$
点评 本题考查余弦定理,涉及两点间的距离公式,属基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届重庆市高三理上适应性考试一数学试卷(解析版) 题型:选择题
记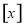 表示不超过
表示不超过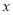 的最大整数,如
的最大整数,如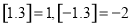 .设函数
.设函数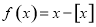 ,若方程
,若方程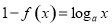 有且仅有3个实数根,则正实数
有且仅有3个实数根,则正实数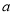 的取值范围为( )
的取值范围为( )
A.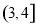 B.
B.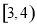 C.
C. D.
D.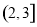
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com