
分析 根据抽象函数的关系式,采用赋值法,可解决①②,在此基础上继续对各个选项逐一验证可得答案.
解答 解:①令x=y=0,
则f(0)=f(0)+f(0)+$\frac{1}{2}$,
即f(0)=-$\frac{1}{2}$,故①正确,
②令y=x=$\frac{1}{2}$,得f(1)=f($\frac{1}{2}$)+f($\frac{1}{2}$)+$\frac{1}{2}$=$\frac{1}{2}$;
令x=1,y=-1,得f(1-1)=f(1)+f(-1)+$\frac{1}{2}$=f(0),
即$\frac{1}{2}$+f(-1)+$\frac{1}{2}$=-$\frac{1}{2}$;
即f(-1)=-$\frac{3}{2}$,故②正确,
③取y=-1代入可得f(x-1)=f(x)+f(-1)+$\frac{1}{2}$,即f(x-1)-f(x)=f(-1)+$\frac{1}{2}$=-1<0,即f(x-1)<f(x),
故③f(x)为R上减函数,错误;
④令y=-x代入可-$\frac{1}{2}$=f(0)=f(x)+f(-x)+$\frac{1}{2}$,即f(x)+$\frac{1}{2}$+f(-x)+$\frac{1}{2}$=0,故f(x)+$\frac{1}{2}$为奇函数,故④正确,
故正确是①②④,
故答案为:①②④
点评 本题主要考查与函数有关的命题的真假判断,利用赋值法是解决抽象函数常用的一种方法,考查学生的运算和推理能力.


科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | [-1,0] | C. | [-1,1] | D. | [-$\frac{1}{2}$,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -2 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1(x>2) | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1(x<-2) | ||
| C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1(x≠±2) | D. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{12}$=1(x≠±2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
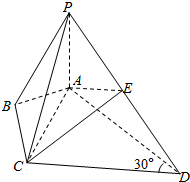 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com