
| A. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{\sqrt{3}}{2}$ |
分析 根据题意和n≥2时,an=sn-sn-1,分别求出a3、a4、a5,再根据比例关系设三角形的三边为3k,5k,7k(k>0),判断出最大角所对的边,利用余弦定理求出余弦值.
解答 解:由Sn=n2-2n+1,得a3=S3-S2=4-1=3,同理得a4=9-4=5,a5=16-9=7,
可设a:b:c=a3:a4:a5,设三角形的三边为3k,5k,7k(k>0),
则边7k所对的角最大,令该三角形最大角为θ,
由余弦定理得,cosθ=$\frac{9{k}^{2}+25{k}^{2}-49{k}^{2}}{2•3k•5k}$=-$\frac{1}{2}$,
故选:B.
点评 本题考查数列中:n≥2时an=Sn-Sn-1的应用,以及余弦定理的应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
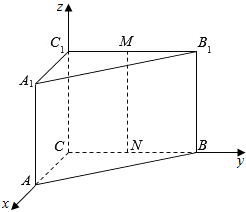 在直三棱柱ABC-A1B1C1中,AC=2,CB=CC1=4,∠BCA=90°,E、F、M、N分别是A1B1、AB、C1B1、CB的中点,建立如图所示的坐标系.
在直三棱柱ABC-A1B1C1中,AC=2,CB=CC1=4,∠BCA=90°,E、F、M、N分别是A1B1、AB、C1B1、CB的中点,建立如图所示的坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
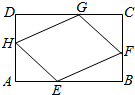 如图,有一块矩形空地ABCD,要在这块空地上开辟一个内接四边形EFGH为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地EFGH面积为y.
如图,有一块矩形空地ABCD,要在这块空地上开辟一个内接四边形EFGH为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地EFGH面积为y.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
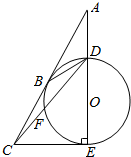 如图,由圆O外一点A引圆的切线AB和割线ADE,B为切点,DE为圆O的直径,且AD=DB.延长AB至C使得CE与圆O相切,连结CD交圆O于点F.
如图,由圆O外一点A引圆的切线AB和割线ADE,B为切点,DE为圆O的直径,且AD=DB.延长AB至C使得CE与圆O相切,连结CD交圆O于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y-3=0 | B. | x+y-3=0或2x+5y=0 | ||
| C. | x-y-7=0或2x+5y=0 | D. | x-y-7=0或x+y-3=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com