
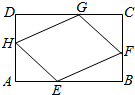
 如图,有一块矩形空地ABCD,要在这块空地上开辟一个内接四边形EFGH为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地EFGH面积为y.
如图,有一块矩形空地ABCD,要在这块空地上开辟一个内接四边形EFGH为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地EFGH面积为y.分析 (1)求得S△AEH=S△CGF=$\frac{1}{2}$x2,S△BEF=S△DGH=$\frac{1}{2}$(a-x)(2-x),利用y=SABCD-2(S△AEH+S△BEF),化简即得结论;
(2)通过(1)可知y=-2x2+(a+2)x的图象为开口向下、对称轴是x=$\frac{a+2}{4}$的抛物线,比较$\frac{a+2}{4}$与2的大小关系并结合函数的单调性即得结论.
解答 解:(1)由AE=AH=CF=CG,
依题意,S△AEH=S△CGF=$\frac{1}{2}$x2,
S△BEF=S△DGH=$\frac{1}{2}$(a-x)(2-x),
则y=SABCD-2S△AEH-2S△BEF=2a-x2-(a-x)(2-x)=-2x2+(a+2)x,
由题意$\left\{\begin{array}{l}{x>0}\\{a-x>0}\\{2-x≥0}\\{a>2}\end{array}\right.$,解得:0<x≤2,
∴y=-2x2+(a+2)x,其中定义域为(0,2];
(2)∵y=-2x2+(a+2)x的图象为抛物线,其开口向下、对称轴是x=$\frac{a+2}{4}$,
∴y=-2x2+(a+2)x在(0,$\frac{a+2}{4}$)递增,在($\frac{a+2}{4}$,+∞)上递减.
若$\frac{a+2}{4}$<2,即a<6,则x=$\frac{a+2}{4}$时,y取最大值$\frac{(a+2)^{2}}{8}$;
若$\frac{a+2}{4}$≥2,即a≥6,则y=-2x2+(a+2)x,0<x≤2是增函数,
故当x=2时,y取最大值2a-4;
综上所述:若a<6,则AE=$\frac{a+2}{4}$时绿地面积取最大值$\frac{(a+2)^{2}}{8}$;
若a≥6,则AE=2时绿地面积取最大值2a-4.
点评 本题考查函数模型的选择与应用,考查分类讨论的思想,注意解题方法的积累,属于中档题.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -2 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1(x>2) | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1(x<-2) | ||
| C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1(x≠±2) | D. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{12}$=1(x≠±2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com