
分析 (1)求导数,确定切线斜率,切点坐标,即可求函数g(x)=f(x)-x-2的图象在x=1处的切线方程;
(2)确定f(x)max=f(1)=ln1-1=-1,|f(x)|min=1,设G(x)=$\frac{lnx}{x}+\frac{1}{2}$,则${G^'}(x)=\frac{1-lnx}{x^2}$,故G(x)在(0,e)上是增加的,在(e,+∞)上是减少的,故$G{(x)_{max}}=G(e)=\frac{1}{e}+\frac{1}{2}<1$,G(x)max<|f(x)|min,即可证明结论;
(3)$\frac{f(m)-f(n)}{m-n}+1=\frac{lnm-lnn-m+n}{m-n}+1=\frac{1}{n}×\frac{{ln\frac{m}{n}}}{{\frac{m}{n}-1}}$,$\frac{m}{{{m^2}+{n^2}}}=\frac{1}{n}×\frac{1}{{\frac{n}{m}+\frac{m}{n}}}$,m>n>0,可得$\frac{m}{n}-1>0$,故只需比较ln$\frac{m}{n}$-$\frac{\frac{m}{n}-1}{\frac{n}{m}+\frac{m}{n}}$与O的大小.
解答 (1)解:因为g(x)=lnx-2(x+1)
所以$g'(x)=\frac{1-2x}{x}$,g'(1)=-1…(1分)
又因g(1)=-4,所以切点为(1,-4)…(2分)
故所求的切线方程为:y+4=-(x-1),即y+x+3=0…(3分)
(2)证明:因为$f'(x)=\frac{1-x}{x}$,所以f(x)在(0,1)上是增加的,在(1,+∞)上是减少的,
所以f(x)max=f(1)=ln1-1=-1,|f(x)|min=1…(4分)
设G(x)=$\frac{lnx}{x}+\frac{1}{2}$,则${G^'}(x)=\frac{1-lnx}{x^2}$,故G(x)在(0,e)上是增加的,在(e,+∞)上是减少的,
故$G{(x)_{max}}=G(e)=\frac{1}{e}+\frac{1}{2}<1$,G(x)max<|f(x)|min
所以$|{f(x)}|>\frac{lnx}{x}+\frac{1}{2}$对任意x∈(0,+∞)恒成立…(7分)
(3)解:$\frac{f(m)-f(n)}{m-n}+1=\frac{lnm-lnn-m+n}{m-n}+1=\frac{1}{n}×\frac{{ln\frac{m}{n}}}{{\frac{m}{n}-1}}$,$\frac{m}{{{m^2}+{n^2}}}=\frac{1}{n}×\frac{1}{{\frac{n}{m}+\frac{m}{n}}}$
∵m>n>0,∴$\frac{m}{n}-1>0$,故只需比较ln$\frac{m}{n}$-$\frac{\frac{m}{n}-1}{\frac{n}{m}+\frac{m}{n}}$与O的大小…(8分)
令$\frac{m}{n}$=t,设G(t)=lnt-$\frac{t-1}{\frac{1}{t}+t}$…(9分)
因为t>1,所以G'(t)>0,所以函数G(t)在(1,+∞)上是增加的,
故G(t)>G(1)=0…(10分)
所以 G(t)>0对任意t>1恒成立…(11分)
即$ln\frac{m}{n}>\frac{{\frac{m}{n}-1}}{{\frac{n}{m}+\frac{m}{n}}}$,从而有$\frac{f(m)-f(n)}{m-n}+1$>$\frac{m}{{{m^2}+{n^2}}}$…(12分)
点评 本题考查导数知识的综合运用,考查函数的单调性,考查导数的几何意义,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
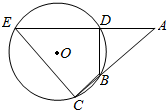 如图,⊙O的弦ED,CB的延长线交于点A.
如图,⊙O的弦ED,CB的延长线交于点A.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
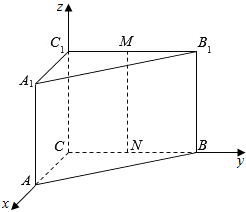 在直三棱柱ABC-A1B1C1中,AC=2,CB=CC1=4,∠BCA=90°,E、F、M、N分别是A1B1、AB、C1B1、CB的中点,建立如图所示的坐标系.
在直三棱柱ABC-A1B1C1中,AC=2,CB=CC1=4,∠BCA=90°,E、F、M、N分别是A1B1、AB、C1B1、CB的中点,建立如图所示的坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,7] | B. | [-3,7] | C. | (0,$\frac{5}{2}$] | D. | [0,$\frac{5}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
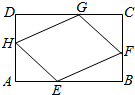 如图,有一块矩形空地ABCD,要在这块空地上开辟一个内接四边形EFGH为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地EFGH面积为y.
如图,有一块矩形空地ABCD,要在这块空地上开辟一个内接四边形EFGH为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地EFGH面积为y.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y-3=0 | B. | x+y-3=0或2x+5y=0 | ||
| C. | x-y-7=0或2x+5y=0 | D. | x-y-7=0或x+y-3=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com