
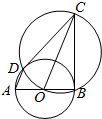 如图所示,直径分别为AB、OC的两圆相交于B、D两点,O为AB的中点.
如图所示,直径分别为AB、OC的两圆相交于B、D两点,O为AB的中点.分析 (1)要证明AD∥OC,我们要根据直线平行的判定定理,观察已知条件及图形,我们可以连接BD、OD,只要证明BD⊥OC,BD⊥AD
即可得证.
(2)因为⊙O的半径为2,而其它线段长均为给出,故要想求AD•OC的值,我们要将其转化用半径相等或相关的线段积的形式,结合(1)的结论,我们易证明Rt△BAD∽Rt△ODC,根据相似三角形性质,不难得到转化的思路.
解答 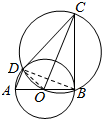 (1)证明:如图,连接BD、OD.
(1)证明:如图,连接BD、OD.
∵直径分别为AB、OC的两圆相交于B、D两点
∴BD⊥OC,BD⊥AD
∴AD∥OC;
(2)解:AO=OD,则∠ODA=∠A=∠DOC,
∴Rt△BAD∽Rt△ODC,
∵圆O的半径为2,
∴AD•OC=AB•OD=8.
点评 根据求证的结论,使用分析推敲证明过程中所需要的条件,进而分析添加辅助线的方法,是平面几何证明必须掌握的技能,大家一定要熟练掌握,而在(2)中根据已知条件分析转化的方向也是解题的主要思想.解决就是寻找解题的思路,由已知出发,找寻转化方向和从结论出发寻找转化方向要结合在一起使用.


科目:高中数学 来源: 题型:选择题
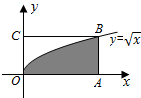 如图,函数$y=\sqrt{x}$的图象过矩形OABC的顶点B,且OA=4.若在矩形OABC内随机地撒100粒豆子,落在图中阴影部分的豆子有67粒,则据此可以估算出图中阴影部分的面积约为( )
如图,函数$y=\sqrt{x}$的图象过矩形OABC的顶点B,且OA=4.若在矩形OABC内随机地撒100粒豆子,落在图中阴影部分的豆子有67粒,则据此可以估算出图中阴影部分的面积约为( )| A. | 2.64 | B. | 2.68 | C. | 5.36 | D. | 6.64 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1(x>2) | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1(x<-2) | ||
| C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1(x≠±2) | D. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{12}$=1(x≠±2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
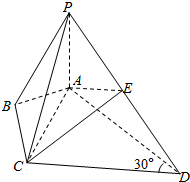 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -12 | B. | -20 | C. | 12 | D. | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com