
分析 (1)通过Sn=$\frac{4}{3}$(an-2)与Sn-1=$\frac{4}{3}$(an-1-2)作差,整理可知an=4an-1(n≥2),进而可知数列{bn}是首项为3、公差为2的等差数列;
(2)通过(1)裂项可知cn=(-1)n+1($\frac{1}{2n+1}$+$\frac{1}{2n+3}$),分n为奇数、偶数两种情况讨论即可.
解答 (1)证明:∵Sn=$\frac{4}{3}$(an-2),
∴当n≥2时,Sn-1=$\frac{4}{3}$(an-1-2),
两式相减得:an=$\frac{4}{3}$(an-an-1),
整理得:an=4an-1(n≥2),
又∵S1=$\frac{4}{3}$(a1-2),即a1=8,
∴数列{an}是首项为8、公比为4的等比数列,
∴bn=log2an=bn=log2(8•4n-1)=log222n+1=2n+1,
于是数列{bn}是首项为3、公差为2的等差数列;
(2)解:由(1)可知$\frac{4(n+1)}{{b}_{n}{b}_{n+1}}$=$\frac{4(n+1)}{(2n+1)(2n+3)}$=$\frac{1}{2n+1}$+$\frac{1}{2n+3}$,
从而cn=(-1)n+1$\frac{4(n+1)}{{b}_{n}{b}_{n+1}}$=(-1)n+1($\frac{1}{2n+1}$+$\frac{1}{2n+3}$),
当n为偶数时,Tn=$\frac{1}{3}$+$\frac{1}{5}$-$\frac{1}{5}$-$\frac{1}{7}$+$\frac{1}{7}$+$\frac{1}{9}$-…+$\frac{1}{2n-1}$+$\frac{1}{2n+1}$-$\frac{1}{2n+1}$-$\frac{1}{2n+3}$
=$\frac{1}{3}$-$\frac{1}{2n+3}$
=$\frac{2n}{3(2n+3)}$;
当n为奇数时,Tn=$\frac{1}{3}$+$\frac{1}{5}$-$\frac{1}{5}$-$\frac{1}{7}$+$\frac{1}{7}$+$\frac{1}{9}$-…-$\frac{1}{2n-1}$-$\frac{1}{2n+1}$+$\frac{1}{2n+1}$+$\frac{1}{2n+3}$
=$\frac{1}{3}$+$\frac{1}{2n+3}$
=$\frac{2n+6}{3(2n+3)}$;
综上所述,Tn=$\left\{\begin{array}{l}{\frac{2n+6}{3(2n+3)},}&{n为奇数}\\{\frac{2n}{3(2n+3)},}&{n为偶数}\end{array}\right.$.
点评 本题考查数列的通项及前n项和,考查分类讨论的思想,考查运算求解能力,注意解题方法的积累,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
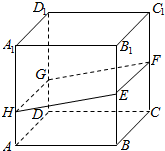 如图,边长为1的正方体ABCD-A1B1C1D1中,E、F分别为BB1、C1C的中点,DG=$\frac{1}{3}$DD1,过E、F、G的平面交AA1于点H,求A1D1到面EFGH的距离.
如图,边长为1的正方体ABCD-A1B1C1D1中,E、F分别为BB1、C1C的中点,DG=$\frac{1}{3}$DD1,过E、F、G的平面交AA1于点H,求A1D1到面EFGH的距离.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com