
| A. | [0,1] | B. | [-1,0] | C. | [-1,1] | D. | [-$\frac{1}{2}$,$\frac{1}{2}$] |
分析 令t=2x,x∈[0,1],则t∈[1,2],y=f(x)=|t-$\frac{a}{t}$|,若函数f(x)=|2x-$\frac{a}{{2}^{x}}$|,其在区间[0,1]上单调递增,则y=|t-$\frac{a}{t}$|,t∈[1,2]为增函数,分类讨论,可得满足条件的a的取值范围.
解答 解:令t=2x,x∈[0,1],则t∈[1,2],y=f(x)=|t-$\frac{a}{t}$|,
若函数f(x)=|2x-$\frac{a}{{2}^{x}}$|,其在区间[0,1]上单调递增,
则y=|t-$\frac{a}{t}$|,t∈[1,2]为增函数,
若a>0,y=|t-$\frac{a}{t}$|的单调递增区间为[-$\sqrt{a}$,0)和[$\sqrt{a}$,+∞),
则$\sqrt{a}$≤1,即0<a≤1
若a=0,y=t,t∈[1,2]为增函数,满足条件;
若a<0,y=|t-$\frac{a}{t}$|的单调递增区间为[-$\sqrt{-a}$,0)和[$\sqrt{-a}$,+∞),
则$\sqrt{-a}$≤1,即-1≤a<0,
综上可得a的取值范围为[-1,1],
故选:C
点评 本题考查的知识点是函数单调性的性质,分类讨论思想,难度中档.


科目:高中数学 来源: 题型:解答题
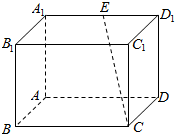 如图所示,在长方体ABCD-A1B1C1D1中,BC=2AB=4,$A{A_1}=2\sqrt{2}$,E是A1D1的中点.
如图所示,在长方体ABCD-A1B1C1D1中,BC=2AB=4,$A{A_1}=2\sqrt{2}$,E是A1D1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
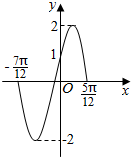
| A. | ω=2 | |
| B. | $f({\frac{π}{3}})=1$ | |
| C. | 函数f(x)的图象关于(-$\frac{11π}{12}$,0)对称 | |
| D. | 函数f(x)的图象向左平移$\frac{11π}{12}$个单位后得到y=Asinωx的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
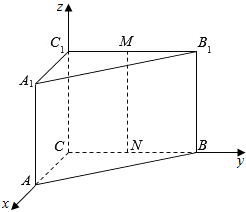 在直三棱柱ABC-A1B1C1中,AC=2,CB=CC1=4,∠BCA=90°,E、F、M、N分别是A1B1、AB、C1B1、CB的中点,建立如图所示的坐标系.
在直三棱柱ABC-A1B1C1中,AC=2,CB=CC1=4,∠BCA=90°,E、F、M、N分别是A1B1、AB、C1B1、CB的中点,建立如图所示的坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,7] | B. | [-3,7] | C. | (0,$\frac{5}{2}$] | D. | [0,$\frac{5}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com