
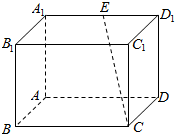
 如图所示,在长方体ABCD-A1B1C1D1中,BC=2AB=4,$A{A_1}=2\sqrt{2}$,E是A1D1的中点.
如图所示,在长方体ABCD-A1B1C1D1中,BC=2AB=4,$A{A_1}=2\sqrt{2}$,E是A1D1的中点.分析 (Ⅰ)连接B1E,C1E,则直线B1E即为所求直线l,推导出B1E⊥CC1,B1E⊥C1E,能证明l⊥CE.
(Ⅱ)连接B1C,则平面CEB1即为平面α,过点C1作C1F⊥CE于F,则C1F⊥平面α,直线CC1和平面α所成角为∠FCC1,由此能求出点C1到平面α的距离.
解答 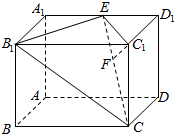 解:(Ⅰ)如图所示,连接B1E,C1E,则直线B1E即为所求直线l…(3分)
解:(Ⅰ)如图所示,连接B1E,C1E,则直线B1E即为所求直线l…(3分)
∵在长方体ABCD-A1B1C1D1中,CC1⊥平面A1B1C1D1
∴B1E⊥CC1…(4分)
∵B1C1=2A1B1=4,E是A1D1的中点
∴B1E⊥C1E…(5分)
又CC1∩C1E=C1
∴B1E⊥平面CC1E
∴B1E⊥CE,即l⊥CE…(6分)
(Ⅱ)如图所示,连接B1C,则平面CEB1即为平面α
过点C1作C1F⊥CE于F…(7分)
由(Ⅰ)知B1E⊥平面CC1E,故B1E⊥C1F
∵C1F⊥CE,CE∩B1E=E
∴C1F⊥平面CEB1,即C1F⊥平面α…(9分)
∴直线CC1和平面α所成角为∠FCC1…(10分)
∵在△ECC1中,$E{C_1}=C{C_1}=2\sqrt{2}$,且EC1⊥CC1
∴C1F=2…(11分)
∴点C1到平面α的距离为2…(12分)
点评 本题考查线面垂直的作法与证明,考查点到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源:2015-2016学年辽宁大连十一中高一下学期段考二试数学(文)试卷(解析版) 题型:选择题
某产品的广告费用x与销售额y的统计数据如下表:
广告费用x(万元) | 4 | 2 | 3 | 5 |
销售额y(万元) | 49 | 26 | 39 | 54 |
根据上表可得回归方程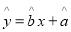 中的
中的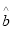 为
为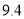 ,据此模型预报广告费用为6万元时销售额为 ( )
,据此模型预报广告费用为6万元时销售额为 ( )
A. 63.6万元 B. 65.5万元 C. 67.7万元 D. 72.0万元
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
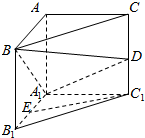 在直三棱柱ABC-A1B1C1中,∠BAC=90°,D,E分别为CC1和A1B1的中点,且A1A=AC=2AB=2.
在直三棱柱ABC-A1B1C1中,∠BAC=90°,D,E分别为CC1和A1B1的中点,且A1A=AC=2AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
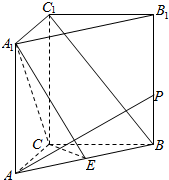 如图,在三棱柱ABC-A1B1C1中,AC=CB=2,且AC⊥CB,AA1⊥底面ABC,E为AB中点.
如图,在三棱柱ABC-A1B1C1中,AC=CB=2,且AC⊥CB,AA1⊥底面ABC,E为AB中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
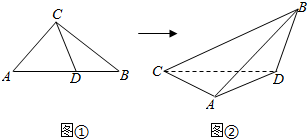
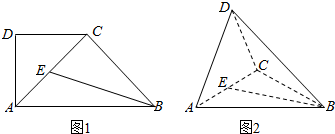 如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AD=CD=$\frac{1}{2}$AB=2,点E为AC中点.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2所示.
如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AD=CD=$\frac{1}{2}$AB=2,点E为AC中点.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
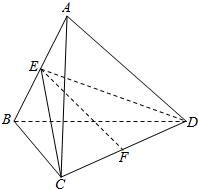 如图,正四面体ABCD的棱长为1.
如图,正四面体ABCD的棱长为1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | [-1,0] | C. | [-1,1] | D. | [-$\frac{1}{2}$,$\frac{1}{2}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com