
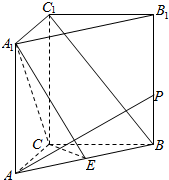
 如图,在三棱柱ABC-A1B1C1中,AC=CB=2,且AC⊥CB,AA1⊥底面ABC,E为AB中点.
如图,在三棱柱ABC-A1B1C1中,AC=CB=2,且AC⊥CB,AA1⊥底面ABC,E为AB中点.分析 (Ⅰ)推忸出AA1⊥CB,AC⊥CB,由此能证明CB⊥A1C.
(Ⅱ)连接AC1与A1C交于点F,连接EF,推导出四边形AA1C1C是平行四边形,从而EF∥C1B,由此能证明BC1∥平面A1CE.
(Ⅲ)过P作PQ∥BC,交CC1于Q,由PQ⊥面ACC1A1,CQ=a,能求出结果.
解答 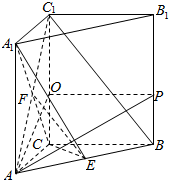 证明:(Ⅰ)因为AA1⊥底面ABC,所以AA1⊥CB.(2分)
证明:(Ⅰ)因为AA1⊥底面ABC,所以AA1⊥CB.(2分)
因为AC⊥CB,所以CB⊥平面AA1C1C.(4分)
所以CB⊥A1C.(5分)
(Ⅱ)连接AC1与A1C交于点F,连接EF,(7分)
由三棱柱性质可得四边形AA1C1C是平行四边形,
所以点F是AC1的中点.
因为E为AB中点,
所以在△AC1B中,EF∥C1B.(8分)
因为EF?平面A1CE,BC1?平面A1CE,(10分)
所以BC1∥平面A1CE.(11分)
解:(Ⅲ)$a=\frac{4}{3}$.(14分)
点评 本题考查线线垂直、线面平行的证明,考查线段长的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源:2015-2016学年辽宁大连十一中高一下学期段考二试数学(文)试卷(解析版) 题型:选择题
从1,2,3,4,5这5个数字中,不放回地任取两数,则两数都是奇数的概率是( )
A.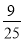 B.
B.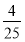 C.
C.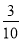 D.
D.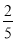
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
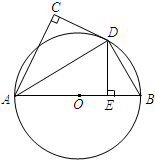 如图,AB为⊙O的直径,直线CD与⊙O相切于点D,AC⊥CD,DE⊥AB,C、E为垂足,连接AD,BD.若AC=4,DE=3,求BD的长.
如图,AB为⊙O的直径,直线CD与⊙O相切于点D,AC⊥CD,DE⊥AB,C、E为垂足,连接AD,BD.若AC=4,DE=3,求BD的长.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
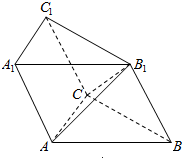 如图,已知斜三棱柱ABC-A1B1C1中,底面ABC是等边三角形,侧面BB1C1C是菱形,∠B1BC=60°.
如图,已知斜三棱柱ABC-A1B1C1中,底面ABC是等边三角形,侧面BB1C1C是菱形,∠B1BC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
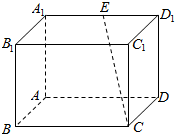 如图所示,在长方体ABCD-A1B1C1D1中,BC=2AB=4,$A{A_1}=2\sqrt{2}$,E是A1D1的中点.
如图所示,在长方体ABCD-A1B1C1D1中,BC=2AB=4,$A{A_1}=2\sqrt{2}$,E是A1D1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{y^2}{2}-\frac{x^2}{4}=1$ | B. | $\frac{x^2}{4}-\frac{y^2}{2}=1$ | C. | $\frac{y^2}{4}-\frac{x^2}{2}=1$ | D. | $\frac{x^2}{2}-\frac{y^2}{4}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
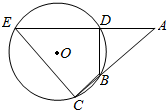 如图,⊙O的弦ED,CB的延长线交于点A.
如图,⊙O的弦ED,CB的延长线交于点A.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com