练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
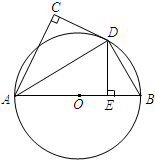
    3．如图，AB为⊙O的直径，直线CD与⊙O相切于点D，AC⊥CD，DE⊥AB，C、E为垂足，连接AD，BD．若AC=4，DE=3，求BD的长．

    分析 先证明△EDA∽△DBA，再证明△ACD≌△AED，即可得出结论．

    解答 解：因为CD与⊙O相切于点D，所以∠CDA=∠DBA，…（2分）
    又因为AB为⊙O的直径，所以∠ADB=90°．
    又DE⊥AB，所以△EDA∽△DBA，
    所以∠EDA=∠DBA，所以∠EDA=∠CDA．…（4分）
    又∠ACD=∠AED=90°，AD=AD，所以△ACD≌△AED．
    所以AE=AC=4，所以AD=5，…（6分）
    又$\frac{DE}{BD}$=$\frac{AE}{AD}$，所以BD=$\frac{15}{4}$．…（10分）

    点评 本题考查三角形相似的判定与性质，考查三角形全等的证明，考查学生分析解决问题的能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015-2016学年辽宁大连十一中高一下学期段考二试数学（文）试卷（解析版） 题型：填空题

    ①函数y＝cos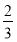（x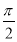＋）是奇函数；

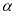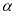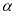    ②存在实数，使得sin＋cos＝2；

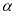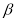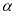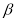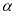    ③若、是第一象限角且<，则tan<tan；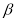

    ④x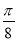＝是函数y＝sin（2x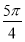＋）的一条对称轴方程；

    ⑤函数y＝tan（2x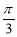＋）的图象关于点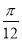（，0）成中心对称图形．

    其中正确命题的序号为__________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知正三棱柱的侧面展开图是相邻边长分别为3和6的矩形，则该正三棱柱的体积是$\frac{3\sqrt{3}}{2}或3\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知双曲线C：${x^2}-\frac{y^2}{{{3^{\;}}}}=1$，A、B是双曲线上关于原点对称的两点，M是双曲线上异于A、B的一点，直线MA、MB的斜率分别记为k1，k2，且k1∈[-3，-1]，则k2的取值范围是[-3，-1]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

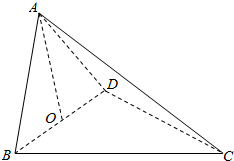    19．如图，四面体ABCD中，O是BD的中点，△ABD和△BCD均为等边三角形，AB=2，AC=$\sqrt{6}$．
    （Ⅰ）求证：AO⊥平面BCD；
    （Ⅱ）求O点到平面ACD的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

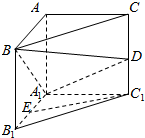    8．在直三棱柱ABC-A1B1C1中，∠BAC=90°，D，E分别为CC1和A1B1的中点，且A1A=AC=2AB=2．
    （1）求证：C1E∥面A1BD；
    （2）求点C1到平面A1BD的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

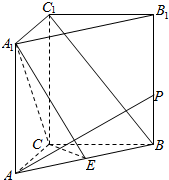    14．如图，在三棱柱ABC-A1B1C1中，AC=CB=2，且AC⊥CB，AA1⊥底面ABC，E为AB中点．
    （Ⅰ）求证：BC⊥A1C；
    （Ⅱ）求证：BC1∥平面A1CE；
    （Ⅲ）若AA1=3，BP=a，且AP⊥A1C，写出a的值（不需写过程）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

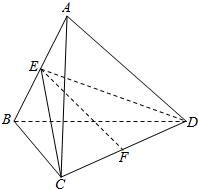    11．如图，正四面体ABCD的棱长为1．
    （1）求异面直线AB、CD之间的距离；
    （2）求点A到平面BCD的距离；
    （3）求点E到平面ACD的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．执行如图的框图，若输入k=30，则输出的n=（　　）
    A．4B．5C．6D．7

    查看答案和解析>>

    同步练习册答案