
分析 (1)点A的极坐标为($\sqrt{2}$,$\frac{5π}{4}$),直线1的极坐标方程为ρcos(θ-$\frac{π}{4}$)=a,且点A在直线1上,代入可得a.把直线1的极坐标方程展开,代入$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$即可得出直角坐标方程.
(2)曲线C的极坐标方程为ρ+sinθ=0,可得ρ2+ρsinθ=0,可得直角坐标方程:x2+y2+y=0,配方为:${x}^{2}+(y+\frac{1}{2})^{2}$=$\frac{1}{4}$,可得圆心C$(0,-\frac{1}{2})$,半径r=$\frac{1}{2}$.求出圆心C到直线l的距离d,把d与r比较即可得出.
解答 解:(1)点A的极坐标为($\sqrt{2}$,$\frac{5π}{4}$),直线1的极坐标方程为ρcos(θ-$\frac{π}{4}$)=a,且点A在直线1上,
∴$\sqrt{2}cos(\frac{5π}{4}-\frac{π}{4})$=-$\sqrt{2}$=a,
∴直线1的极坐标方程为ρcos(θ-$\frac{π}{4}$)=-$\sqrt{2}$,
展开为:$\frac{\sqrt{2}}{2}(ρcosθ+ρsinθ)$=-$\sqrt{2}$,可得直角坐标方程:x+y+2=0.
(2)曲线C的极坐标方程为ρ+sinθ=0,可得ρ2+ρsinθ=0,
可得直角坐标方程:x2+y2+y=0,
配方为:${x}^{2}+(y+\frac{1}{2})^{2}$=$\frac{1}{4}$,可得圆心C$(0,-\frac{1}{2})$,半径r=$\frac{1}{2}$.
∴圆心C到直线l的距离d=$\frac{|0-\frac{1}{2}+2|}{\sqrt{2}}$=$\frac{3\sqrt{2}}{4}$$>\frac{1}{2}$=r.
∴断直线l与曲线C的位置是相离关系.
点评 本题考查了极坐标方程化为直角坐标方程的方法、直线与圆的位置关系的判定方法、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 四棱锥四个侧面中不存在两组侧面互相垂直 | |
| B. | 四棱锥的四个侧面可能全是直角三角形 | |
| C. | 若该四棱锥的左视图为直角三角形,则体积为$\frac{4}{3}$ | |
| D. | 若该四棱锥的正视图为等腰三角形,则四棱锥的侧面积为6+2$\sqrt{2}$+2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
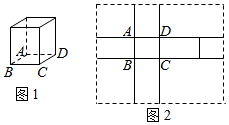 图2中的实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD是边长为1的正方形,若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是$\frac{1}{4}$.
图2中的实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD是边长为1的正方形,若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com