
分析 (1)设点A(x1,y1),D(x2,y2),则B(-x1,-y1),代入椭圆方程可得$\frac{{x}_{1}^{2}}{{a}^{2}}+\frac{{y}_{1}^{2}}{{b}^{2}}$=1,$\frac{{x}_{2}^{2}}{{a}^{2}}+\frac{{y}_{2}^{2}}{{b}^{2}}$=1由AD⊥AB,可得kAD=-$\frac{1}{k}$,利用斜率计算公式可得:$-\frac{1}{k}$=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$,$\frac{1}{4}k$=$\frac{{y}_{2}+{y}_{1}}{{x}_{2}+{x}_{1}}$,相乘可得:$\frac{{b}^{2}}{{a}^{2}}=\frac{1}{4}$,又a2-b2=3,联立解出即可得出.
(2)$\frac{{y}_{1}}{{x}_{1}}$=k,可得直线l2的方程为:y+y1=$\frac{{y}_{1}}{4{x}_{1}}$(x+x1),分别令x=0,y=0,可得S△OMN=$\frac{1}{2}|OM||ON|$=$\frac{9}{8}$|x1y1|,由1=$\frac{{x}_{1}^{2}}{4}$+${y}_{1}^{2}$利用基本不等式的性质即可得出.
解答 解:(1)设点A(x1,y1),D(x2,y2),则B(-x1,-y1),
则$\frac{{x}_{1}^{2}}{{a}^{2}}+\frac{{y}_{1}^{2}}{{b}^{2}}$=1,$\frac{{x}_{2}^{2}}{{a}^{2}}+\frac{{y}_{2}^{2}}{{b}^{2}}$=1
∵AD⊥AB,∴kAD=-$\frac{1}{k}$,
因此$-\frac{1}{k}$=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$,$\frac{1}{4}k$=$\frac{{y}_{2}+{y}_{1}}{{x}_{2}+{x}_{1}}$,
∴$-\frac{1}{4}$=$\frac{{y}_{2}^{2}-{y}_{1}^{2}}{{x}_{2}^{2}-{x}_{1}^{2}}$=$\frac{-\frac{{b}^{2}}{{a}^{2}}({x}_{2}^{2}-{x}_{1}^{2})}{{x}_{2}^{2}-{x}_{1}^{2}}$,化为$\frac{{b}^{2}}{{a}^{2}}=\frac{1}{4}$,
又a2-b2=3,
解得a2=4,b2=1.
∴椭圆C的方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1.
(2)∵$\frac{{y}_{1}}{{x}_{1}}$=k,
∴直线l2的方程为:y+y1=$\frac{{y}_{1}}{4{x}_{1}}$(x+x1),
令y=0得xM=3x1,令x=0,得yN=-$\frac{3}{4}{y}_{1}$,
∴S△OMN=$\frac{1}{2}|OM||ON|$=$\frac{9}{8}$|x1y1|,
∵1=$\frac{{x}_{1}^{2}}{4}$+${y}_{1}^{2}$≥|x1y1|,且当|x1|=2|y1|时,取等号,
∴△OMN面积的最大值是$\frac{9}{8}$.
点评 本题考查了椭圆的标准方程及其性质、斜率计算公式、直线方程、三角形面积计算公式、基本不等式的性质,考查了推理能力与计算能力,属于难题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x≤1} | B. | {x|-1≤x<1} | C. | {x|-1<x≤1} | D. | {x|-1≤x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
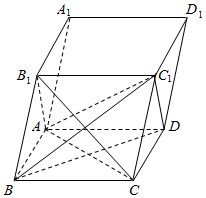 如图,斜四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形,侧面AA1B1B⊥底面ABCD,AA1=2,∠B1BA=60°.
如图,斜四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形,侧面AA1B1B⊥底面ABCD,AA1=2,∠B1BA=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com