
【题目】(1)3个人坐在有八个座位的一排椅子上,若每个人的左右两边都要有空位,则不同坐法的种数为多少?
(2)某高校现有10个保送上大学的名额分配给7所高中学校,若每所高中学校至少有1个名额,则名额分配的方法共有多少种?
【答案】(1)24;(2)84
【解析】
(1)根据题意,使用插空法,把3个人看成是坐在座位上的人,往5个空座的空档插,由组合知识,分析可得答案;
(2)分析题意,可将原问题转化为10个元素之间有9个间隔,要求分成7份,每份不空,使用插空法,相当于用6块档板插在9个间隔中,计算可得答案.
解:(1)由题意知有5个座位都是空的,
我们把3个人看成是坐在座位上的人,往5个空座的空档插,
由于这5个空座位之间共有4个空,3个人去插,
共有![]() (种
(种![]() .
.
(2)根据题意,将10个名额,分配给7所学校,每校至少有1个名额,
可以转化为10个元素之间有9个间隔,要求分成7份,每份不空;
相当于用6块档板插在9个间隔中,
共有![]() 种不同方法.
种不同方法.
所以名额分配的方法共有84种.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】如图所示,合肥一中积极开展美丽校园建设,现拟在边长为0.6千米的正方形地块![]() 上划出一片三角形地块
上划出一片三角形地块![]() 建设小型生态园,点
建设小型生态园,点![]() 分别在边
分别在边![]() 上.
上.
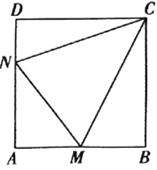
(1)当点![]() 分别时边
分别时边![]() 中点和
中点和![]() 靠近
靠近![]() 的三等分点时,求
的三等分点时,求![]() 的余弦值;
的余弦值;
(2)实地勘察后发现,由于地形等原因,![]() 的周长必须为1.2千米,请研究
的周长必须为1.2千米,请研究![]() 是否为定值,若是,求此定值,若不是,请说明理由.
是否为定值,若是,求此定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊数学家阿波罗尼奧斯(约公元前262~公元前190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,他证明过这样一个命题:平面内与两定点距离的比为常数k(k>0,k≠1)的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.在平面直角坐标系中,设A(﹣3,0),B(3,0),动点M满足![]() =2,则动点M的轨迹方程为()
=2,则动点M的轨迹方程为()
A. (x﹣5)2+y2=16B. x2+(y﹣5)2=9
C. (x+5)2+y2=16D. x2+(y+5)2=9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M(x,y)满足![]()
(1)求点M的轨迹E的方程;
(2)设过点N(﹣1,0)的直线l与曲线E交于A,B两点,若△OAB的面积为![]() (O为坐标原点).求直线l的方程.
(O为坐标原点).求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且an=![]() (3n+Sn)对一切正整数n成立
(3n+Sn)对一切正整数n成立
(I)证明:数列{3+an}是等比数列,并求出数列{an}的通项公式;
(II)设![]() ,求数列
,求数列![]() 的前n项和Bn;
的前n项和Bn;
查看答案和解析>>
科目:高中数学 来源: 题型:
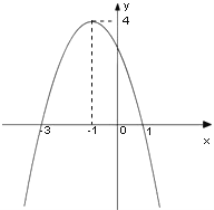
【题目】如图是一个二次函数y=f(x)的图象
(1)写出这个二次函数的零点
(2)求这个二次函数的解析式
(3)当实数k在何范围内变化时,函数g(x)=f(x)-kx在区间[-2,2]上是单调函数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|y=lg(x-![]() )},B={x|
)},B={x|![]() -cx<0,c>0},若AB,则实数c的取值范围是( )
-cx<0,c>0},若AB,则实数c的取值范围是( )
A.(0,1]B.[1,+∞)
C.(0,1)D.(1,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com