
| A. | $\frac{12}{5}$ | B. | $\frac{{9\sqrt{10}}}{5}$ | C. | $\frac{{9\sqrt{2}}}{5}$ | D. | $\frac{{12\sqrt{5}}}{5}$ |
分析 直线$\left\{\begin{array}{l}x=1+2t\\ y=2+t\end{array}$(t是参数),消去参数化为普通方程.利用点到直线的距离公式可得:圆心O(0,0)到直线的距离d,即可得出直线被圆x2+y2=9截得的弦长=2$\sqrt{{r}^{2}-{d}^{2}}$.
解答 解:直线$\left\{\begin{array}{l}x=1+2t\\ y=2+t\end{array}$(t是参数),消去参数化为普通方程:x-2y+3=0.
圆心O(0,0)到直线的距离d=$\frac{3}{\sqrt{5}}$,
∴直线被圆x2+y2=9截得的弦长=2$\sqrt{{r}^{2}-{d}^{2}}$=2$\sqrt{9-(\frac{3}{\sqrt{5}})^{2}}$=$\frac{12\sqrt{5}}{5}$.
故选:D.
点评 本题考查了参数方程与普通方程的互化、点到直线的距离公式、直线与圆相交弦长公式,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 5 | 25 | 30 | 25 | 15 |
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 10 | 20 | 40 | 20 | 10 |
| 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| P(k2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.076 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,在长方体ABCD-A1B1C1D1中,AB=5,AD=8,AA1=4,M为B1C1上一点且B1M=2,点N在线段A1D上,A1D⊥AN.
如图所示,在长方体ABCD-A1B1C1D1中,AB=5,AD=8,AA1=4,M为B1C1上一点且B1M=2,点N在线段A1D上,A1D⊥AN.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
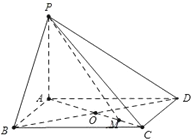 已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为4的菱形,∠BAD=120°,PA=3.
已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为4的菱形,∠BAD=120°,PA=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com