
分析 (1)求出函数的导数,通过讨论a的范围,解关于导函数的不等式,求出函数的递增区间即可;
(2)通过讨论a的范围,结合函数的单调性,判断函数在(1,e]有无零点即可.
解答 解:(1)f(x)的定义域是(0,+∞),
f′(x)=$\frac{1}{x}$-a=$\frac{1-ax}{x}$,
a>0时,由f′(x)>0,解得:0<x<$\frac{1}{a}$,
a≤0时,在(0,+∞)内,f′(x)>0恒成立,
综上,a>0时,f(x)在(0,$\frac{1}{a}$)递增,
a≤0时,f(x)在(0,+∞))递增;
(2)a≤0时,由(1)得f(x)在(0,+∞)递增,
∵f(1)=0,∴此时函数在(1,e]上无零点,符合题意,
0<$\frac{1}{a}$≤1即a≥1时,由(1)知f(x)在(1,e]递减,
∵f(1)=0,得:a≥1时,函数在(1,e]上无零点,符合题意,
$\frac{1}{a}$>1即0<a<1时,若f(x)在(1,e]无零点,由f(1)=0,
结合(1)中函数的单调性可得,只需f(e)>0,即a<$\frac{1}{e-1}$,
此时,0<a<$\frac{1}{e-1}$,
综上,a的范围是(-∞,$\frac{1}{e-1}$)∪[1,+∞).
点评 本题考查了根据导数求函数的单调性、函数的零点问题,考查分类讨论、转化思想以及运算的能力.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{5}$ | B. | $\frac{{9\sqrt{10}}}{5}$ | C. | $\frac{{9\sqrt{2}}}{5}$ | D. | $\frac{{12\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 在平面直角坐标系中,若点P(x,y)的坐标x,y均为整数,对称点P为格点.若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N.边界上的格点数记为L.例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.
在平面直角坐标系中,若点P(x,y)的坐标x,y均为整数,对称点P为格点.若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N.边界上的格点数记为L.例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-5,5] | B. | [3,5] | C. | [3,4] | D. | [2,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
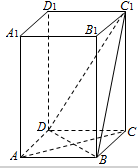 如图,ABCD-A1B1C1D1是正四棱柱.
如图,ABCD-A1B1C1D1是正四棱柱.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com