
分析 (1)曲线C1:$\left\{{\begin{array}{l}{x=-2+cost}\\{y=1+sint}\end{array}$(t为参数),利用平方关系可得曲线C1化为普通方程;C2:$\left\{{\begin{array}{l}{x=-4+\frac{{\sqrt{2}}}{2}s}\\{y=\frac{{\sqrt{2}}}{2}s}\end{array}$(s为参数),消去参数化为普通方程,进而得到曲线形状.
(2)将直线C2的参数方程$\left\{{\begin{array}{l}{x=-4+\frac{{\sqrt{2}}}{2}s}\\{y=\frac{{\sqrt{2}}}{2}s}\end{array}(s为参数)}\right.$代入曲线C1直角坐标方程中,可得${s^2}-3\sqrt{2}s+4=0$,利用根与系数的关系、弦长公式即可得出.
解答 解:(1)曲线C1:$\left\{{\begin{array}{l}{x=-2+cost}\\{y=1+sint}\end{array}$(t为参数),
利用平方关系可得:曲线C1化为普通方程是(x+2)2+(y-1)2=1,
曲线C1是圆心为(-2,1),半径为1的圆;
C2:$\left\{{\begin{array}{l}{x=-4+\frac{{\sqrt{2}}}{2}s}\\{y=\frac{{\sqrt{2}}}{2}s}\end{array}$(s为参数),
消去参数化为普通方程:y=x+4,
曲线C2是斜率为1,在y轴上截距为4的直线.
(2)将直线C2的参数方程$\left\{{\begin{array}{l}{x=-4+\frac{{\sqrt{2}}}{2}s}\\{y=\frac{{\sqrt{2}}}{2}s}\end{array}(s为参数)}\right.$代入曲线${C_1}:{(x+2)^2}+{(y-1)^2}=1$中,
得${s^2}-3\sqrt{2}s+4=0$,
设A,B对应参数分别为s1,s2,
则${s_1}+{s_2}=3\sqrt{2},{s_1}{s_2}=4$,
∴$|{AB}|=|{{s_1}-{s_2}}|=\sqrt{{{({s_1}+{s_2})}^2}-4{s_1}{s_2}}=\sqrt{2}$.
点评 本题考查了参数方程化为普通方程、直线与曲线相交弦长公式、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于中档题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -2016 | B. | -2015 | C. | 2016 | D. | 2015 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 使用年限x(年) | 2 | 3 | 4 | 5 | 6 |
| 维修费用y(万元) | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
| A. | 11.38万元 | B. | 12.38万元 | C. | 13.38万元 | D. | 14.38万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,又知BA1⊥AC1.
已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,又知BA1⊥AC1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
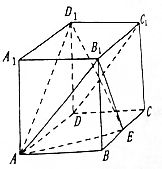 如图,在长方体ABCD-A1B1C1D1中,AB=AA1=1,E为BC中点.
如图,在长方体ABCD-A1B1C1D1中,AB=AA1=1,E为BC中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{5}$ | B. | $\frac{{9\sqrt{10}}}{5}$ | C. | $\frac{{9\sqrt{2}}}{5}$ | D. | $\frac{{12\sqrt{5}}}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com