
如图,某海上缉私小分队驾驶缉私艇以40 km/h的速度由A处出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )

A.5(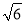 +
+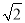 ) km B.5(
) km B.5(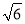 -
- ) km
) km
C.10( -
-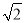 ) km D.10(
) km D.10( +
+ ) km
) km
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-4数系的扩充与复数的引入(解析版) 题型:填空题
已知复数z1=cosθ-i,z2=sinθ+i,则z1·z2的实部的最大值为________,虚部的最大值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-2平面向量的基本定理及坐标表示(解析版) 题型:选择题
在平面直角坐标系xOy中,点A(-1,-2),B(2,3),C(-2,-1),若实数t满足(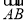 -t
-t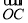 )·
)·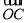 =0,则t的值为( )
=0,则t的值为( )
A.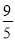 B.-
B.-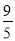 C.
C.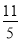 D.-
D.-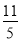
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-1向量的概念及运算(解析版) 题型:选择题
若四边形ABCD满足 +
+ =0,(
=0,( -
-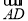 )·
)·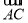 =0,则该四边形一定是( )
=0,则该四边形一定是( )
A.直角梯形 B.菱形 C.矩形 D.正方形
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-8解三角形应用举例(解析版) 题型:解答题
如图,A,B是海面上位于东西方向相距5(3+ )海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20
)海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?

查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-7正弦定理和余弦定理(解析版) 题型:解答题
已知△ABC中,内角A,B,C的对边分别为a,b,c,其中a=2,c=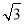 .
.
(1)若sinC=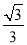 ,求sinA的值;
,求sinA的值;
(2)设f(C)=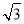 sinCcosC-cos2C,求f(C)的取值范围.
sinCcosC-cos2C,求f(C)的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-7正弦定理和余弦定理(解析版) 题型:填空题
在△ABC中,a,b,c分别是角A,B,C的对边,已知cos2A-3cos(B+C)=1,若△ABC的面积S=5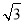 ,b=5,则c的值为________.
,b=5,则c的值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-3三角函数的图象与性质(解析版) 题型:解答题
已知a>0,函数f(x)=-2asin(2x+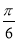 )+2a+b,当x∈[0,
)+2a+b,当x∈[0,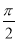 ]时,-5≤f(x)≤1.
]时,-5≤f(x)≤1.
(1)求常数a,b的值;
(2)设g(x)=f(x+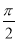 )且lg[g(x)]>0,求g(x)的单调区间.
)且lg[g(x)]>0,求g(x)的单调区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com