
已知△ABC中,内角A,B,C的对边分别为a,b,c,其中a=2,c=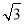 .
.
(1)若sinC=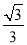 ,求sinA的值;
,求sinA的值;
(2)设f(C)=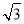 sinCcosC-cos2C,求f(C)的取值范围.
sinCcosC-cos2C,求f(C)的取值范围.
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-1向量的概念及运算(解析版) 题型:解答题
已知点G是△ABO的重心,M是AB边的中点.
(1)求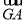 +
+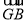 +
+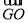 ;
;
(2)若PQ过△ABO的重心G,且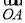 =a,
=a,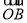 =b,
=b,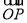 =ma,
=ma,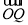 =nb,求证:
=nb,求证: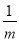 +
+ =3.
=3.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-8解三角形应用举例(解析版) 题型:填空题
在△ABC中,内角A,B,C所对的边分别为a,b,c,其中A=120°,b=1,且△ABC的面积为 ,则
,则 =( )
=( )
A. B.
B.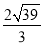 C.2
C.2 D.2
D.2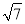
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-8解三角形应用举例(解析版) 题型:选择题
如图,某海上缉私小分队驾驶缉私艇以40 km/h的速度由A处出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )

A.5(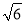 +
+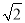 ) km B.5(
) km B.5(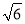 -
- ) km
) km
C.10( -
-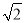 ) km D.10(
) km D.10( +
+ ) km
) km
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-7正弦定理和余弦定理(解析版) 题型:解答题
在△ABC中,内角A,B,C的对边分别为a,b,c.已知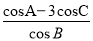 =
= .
.
(1)求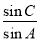 的值;
的值;
(2)若B为钝角,b=10,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-7正弦定理和余弦定理(解析版) 题型:选择题
△ABC的内角A,B,C的对边分别为a,b,c,已知cos(A-C)+cosB=1,a=2c,则C=( )
A. 或
或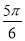 B.
B. C.
C. 或
或 D.
D.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-6简单的三角恒等变换(解析版) 题型:选择题
若α∈(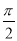 ,π),tan(α+
,π),tan(α+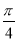 )=
)= ,则sinα=( )
,则sinα=( )
A.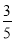 B.
B. C.-
C.-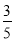 D.-
D.-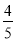
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-3三角函数的图象与性质(解析版) 题型:填空题
设函数f(x)=3sin(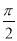 x+
x+ ),若存在这样的实数x1,x2,对任意的x∈R,都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为________.
),若存在这样的实数x1,x2,对任意的x∈R,都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com