
在△ABC中,内角A,B,C所对的边分别为a,b,c,其中A=120°,b=1,且△ABC的面积为 ,则
,则 =( )
=( )
A. B.
B.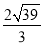 C.2
C.2 D.2
D.2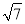
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-1数列的概念与简单表示法(解析版) 题型:填空题
已知数列{an}满足:a4n-3=1,a4n-1=0,a2n=an,n∈N*,则a2009=________;a2014=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-2平面向量的基本定理及坐标表示(解析版) 题型:解答题
已知向量a=(cosθ,sinθ),θ∈[0,π],向量b=(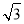 ,-1).
,-1).
(1)若a⊥b,求θ的值;
(2)若|2a-b|<m恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-1向量的概念及运算(解析版) 题型:填空题
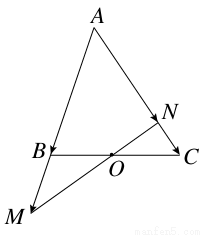
如图所示,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点M,N,若 =m
=m ,
,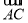 =n
=n ,则m+n的值为________.
,则m+n的值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-1向量的概念及运算(解析版) 题型:选择题
若四边形ABCD满足 +
+ =0,(
=0,( -
-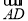 )·
)·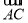 =0,则该四边形一定是( )
=0,则该四边形一定是( )
A.直角梯形 B.菱形 C.矩形 D.正方形
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-8解三角形应用举例(解析版) 题型:填空题
已知A船在灯塔C北偏东80°处,且A船到灯塔C的距离为2 km,B船在灯塔C北偏西40°处,A、B两船间的距离为3 km,则B船到灯塔C的距离为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-7正弦定理和余弦定理(解析版) 题型:解答题
已知△ABC中,内角A,B,C的对边分别为a,b,c,其中a=2,c=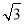 .
.
(1)若sinC=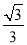 ,求sinA的值;
,求sinA的值;
(2)设f(C)=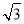 sinCcosC-cos2C,求f(C)的取值范围.
sinCcosC-cos2C,求f(C)的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-6简单的三角恒等变换(解析版) 题型:填空题
设α∈(0,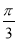 ),β∈(
),β∈(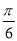 ,
,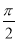 ),且5
),且5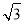 sinα+5cosα=8,
sinα+5cosα=8,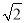 sinβ+
sinβ+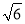 cosβ=2,则cos(α+β)的值为________.
cosβ=2,则cos(α+β)的值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:选择题
函数y=Asin(ωx+φ)(ω>0,|φ|≤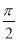 )的部分图象如图所示,则函数的一个表达式为( )
)的部分图象如图所示,则函数的一个表达式为( )
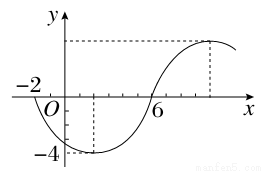
A.y=-4sin(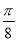 x+
x+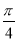 )
)
B.y=4sin( x-
x-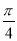 )
)
C.y=-4sin( x-
x-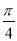 )
)
D.y=4sin(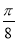 x+
x+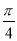 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com