
已知向量a=(cosθ,sinθ),θ∈[0,π],向量b=(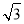 ,-1).
,-1).
(1)若a⊥b,求θ的值;
(2)若|2a-b|<m恒成立,求实数m的取值范围.
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-3等比数列及其前n项和(解析版) 题型:选择题
设{an}是由正数组成的等比数列,Sn为其前n项和.已知a2·a4=1,S3=7,则S5=( )
A.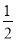 B.
B.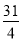 C.
C.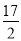 D.
D.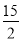
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-3平面向量的数量积及应用(解析版) 题型:填空题
设向量a,b满足|a|=1,|a-b|=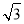 ,a·(a-b)=0,则|2a+b|=________.
,a·(a-b)=0,则|2a+b|=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-3平面向量的数量积及应用(解析版) 题型:选择题
已知a,b,c是平面向量,下列命题中真命题的个数是( )
①(a·b)·c=a·(b·c);
②|a·b|=|a|·|b|;
③|a+b|2=(a+b)2;
④a·b=b·c ⇒a=c
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-2平面向量的基本定理及坐标表示(解析版) 题型:填空题
已知向量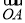 =(k,12),
=(k,12),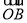 =(4,5),
=(4,5),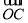 =(-k,10)且A,B,C三点共线,则k=________.
=(-k,10)且A,B,C三点共线,则k=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-1向量的概念及运算(解析版) 题型:解答题
已知点G是△ABO的重心,M是AB边的中点.
(1)求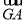 +
+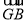 +
+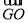 ;
;
(2)若PQ过△ABO的重心G,且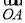 =a,
=a,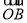 =b,
=b,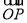 =ma,
=ma,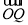 =nb,求证:
=nb,求证: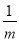 +
+ =3.
=3.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-8解三角形应用举例(解析版) 题型:填空题
在△ABC中,内角A,B,C所对的边分别为a,b,c,其中A=120°,b=1,且△ABC的面积为 ,则
,则 =( )
=( )
A. B.
B.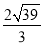 C.2
C.2 D.2
D.2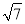
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-6简单的三角恒等变换(解析版) 题型:选择题
若α∈(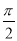 ,π),tan(α+
,π),tan(α+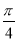 )=
)= ,则sinα=( )
,则sinα=( )
A.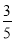 B.
B. C.-
C.-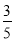 D.-
D.-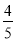
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com